题目内容
3. 如图,O是正△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:
如图,O是正△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;
②点O与O′的距离为4;
③∠AOB=150°;
④S四边形AOBO′=6+3$\sqrt{3}$;
其中正确的结论是( )
| A. | ①②③ | B. | ①③④ | C. | ②③④ | D. | ①② |
分析 证明△BO′A≌△BOC,又∠OBO′=60°,所以△BO′A可以由△BOC绕点B逆时针旋转60°得到,故结论①正确;
由△OBO′是等边三角形,可知结论②正确;
在△AOO′中,三边长为3,4,5,这是一组勾股数,故△AOO′是直角三角形;进而求得∠AOB=150°,故结论③正确;
S四边形AOBO′=S△AOO′+S△OBO′=$\frac{1}{2}$×3×4+$\frac{\sqrt{3}}{4}$×42=6+4$\sqrt{3}$,故结论④错误.
解答 解:如图,
由题意可知,∠1+∠2=∠3+∠2=60°,
∴∠1=∠3,
又∵OB=O′B,AB=BC,
∴△BO′A≌△BOC,
又∵∠OBO′=60°,
∴△BO′A可以由△BOC绕点B逆时针旋转60°得到,
故结论①正确;
如图,连接OO′,
∵OB=O′B,且∠OBO′=60°,
∴△OBO′是等边三角形,
∴OO′=OB=4.
故结论②正确;
∵△BO′A≌△BOC,
∴O′A=5.
在△AOO′中,三边长为3,4,5,这是一组勾股数,
∴△AOO′是直角三角形,∠AOO′=90°,
∴∠AOB=∠AOO′+∠BOO′=90°+60°=150°,
故结论③正确;
S四边形AOBO′=S△AOO′+S△OBO′=$\frac{1}{2}$×3×4+$\frac{\sqrt{3}}{4}$×42=6+4$\sqrt{3}$,
故结论④错误;
故选:A.
点评 本题考查了旋转变换中等边三角形,直角三角形的性质.利用勾股定理的逆定理,判定勾股数3、4、5所构成的三角形是直角三角形,这是本题的要点.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
13. 如图,AB∥CD,CE平分∠ACD交AB于E,若∠A=120°,则∠AEC=( )
如图,AB∥CD,CE平分∠ACD交AB于E,若∠A=120°,则∠AEC=( )
 如图,AB∥CD,CE平分∠ACD交AB于E,若∠A=120°,则∠AEC=( )
如图,AB∥CD,CE平分∠ACD交AB于E,若∠A=120°,则∠AEC=( )| A. | 20° | B. | 25° | C. | 30° | D. | 50° |
14. 如图,把正方形ABCD绕它的中心O顺时针旋转,得到正方形A′B′C′D′,旋转角大于0°小于90°,△A′EF的面积为S,线段AE的长度为x,那么S关于x的函数的图象可能是( )
如图,把正方形ABCD绕它的中心O顺时针旋转,得到正方形A′B′C′D′,旋转角大于0°小于90°,△A′EF的面积为S,线段AE的长度为x,那么S关于x的函数的图象可能是( )
 如图,把正方形ABCD绕它的中心O顺时针旋转,得到正方形A′B′C′D′,旋转角大于0°小于90°,△A′EF的面积为S,线段AE的长度为x,那么S关于x的函数的图象可能是( )
如图,把正方形ABCD绕它的中心O顺时针旋转,得到正方形A′B′C′D′,旋转角大于0°小于90°,△A′EF的面积为S,线段AE的长度为x,那么S关于x的函数的图象可能是( )| A. |  | B. |  | C. |  | D. |  |
18.若A(-$\frac{13}{4}$,y1),B(-$\frac{5}{4}$,y2),C($\frac{1}{4}$,y3)为二次函数y=-x2+4x-5的图象上的三点,则y1,y2,y3的大小关系是( )
| A. | y1<y2<y3 | B. | y2<y1<y3 | C. | y3<y1<y2 | D. | y1<y3<y2 |
8. 如图所示,在△ABD和△ACE中,AB=AC,AD=AE,要证△ABD≌△ACE,需补充的条件是( )
如图所示,在△ABD和△ACE中,AB=AC,AD=AE,要证△ABD≌△ACE,需补充的条件是( )
 如图所示,在△ABD和△ACE中,AB=AC,AD=AE,要证△ABD≌△ACE,需补充的条件是( )
如图所示,在△ABD和△ACE中,AB=AC,AD=AE,要证△ABD≌△ACE,需补充的条件是( )| A. | ∠B=∠C | B. | ∠D=∠E | C. | ∠DAE=∠BAC | D. | ∠CAD=∠DAC |
15.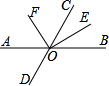 如图,直线AB、CD相交于点O,OF平分∠AOC,OF⊥OE于点O,若∠AOD=70°,则∠COE等于( )
如图,直线AB、CD相交于点O,OF平分∠AOC,OF⊥OE于点O,若∠AOD=70°,则∠COE等于( )
 如图,直线AB、CD相交于点O,OF平分∠AOC,OF⊥OE于点O,若∠AOD=70°,则∠COE等于( )
如图,直线AB、CD相交于点O,OF平分∠AOC,OF⊥OE于点O,若∠AOD=70°,则∠COE等于( )| A. | 35° | B. | 45° | C. | 55° | D. | 65° |
12.下列语句正确的有( )
①直径是弦;
②半圆是弧;
③长度相等的弧是等弧;
④经过圆内一定点可以作无数条弦;
⑤经过圆内一定点可以作无数条直径.
①直径是弦;
②半圆是弧;
③长度相等的弧是等弧;
④经过圆内一定点可以作无数条弦;
⑤经过圆内一定点可以作无数条直径.
| A. | 3 个 | B. | 2个 | C. | 1 个 | D. | 4个 |
13.一个凸多边形的每一个内角都等于140°,那么从这个多边形的一个顶点引出的对角线条数是( )
| A. | 5条 | B. | 6条 | C. | 9条 | D. | 27条 |
 如图,在离铁塔150m的A处,用测倾仪测得塔顶的仰角为30°12′,测倾仪高AD为1.52m,求铁塔高BC(精确到0.1m).
如图,在离铁塔150m的A处,用测倾仪测得塔顶的仰角为30°12′,测倾仪高AD为1.52m,求铁塔高BC(精确到0.1m).