题目内容
15．
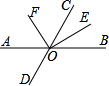如图，直线AB、CD相交于点O，OF平分∠AOC，OF⊥OE于点O，若∠AOD=70°，则∠COE等于（ ）| A． | 35° | B． | 45° | C． | 55° | D． | 65° |
分析 先由邻补角定义求出∠AOC=180°-∠AOD=110°，再根据角平分线定义求出∠COF=$\frac{1}{2}$∠AOC=55°，然后利用垂直定义即可求出∠COE的度数．
解答 解：∵∠AOD=70°，
∴∠AOC=180°-∠AOD=110°，
∵OF平分∠AOC，
∴∠COF=$\frac{1}{2}$∠AOC=55°，
∵OF⊥OE于点O，
∴∠COE=90°-∠COF=35°．
故选A．
点评 本题利用垂直的定义，邻补角定义和角平分线的定义计算，要注意领会由垂直得直角这一要点．
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
5．下面给出的四个图中，表示数轴正确的是（ ）
| A． |  | B． |  | C． |  | D． |  |
6．下列各数对中，数值相等的是（ ）
| A． | +3与+（-3） | B． | -2与-（-2） | C． | -（-3）与+（+3） | D． | -（-3）与-|-3| |
3．
如图，O是正△ABC内一点，OA=3，OB=4，OC=5，将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′，下列结论：
①△BO′A可以由△BOC绕点B逆时针旋转60°得到；
②点O与O′的距离为4；
③∠AOB=150°；
④S四边形AOBO′=6+3$\sqrt{3}$；
其中正确的结论是（ ）
如图，O是正△ABC内一点，OA=3，OB=4，OC=5，将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′，下列结论：①△BO′A可以由△BOC绕点B逆时针旋转60°得到；
②点O与O′的距离为4；
③∠AOB=150°；
④S四边形AOBO′=6+3$\sqrt{3}$；
其中正确的结论是（ ）
| A． | ①②③ | B． | ①③④ | C． | ②③④ | D． | ①② |
20．计算（$\frac{2}{3}$）2015×（$\frac{3}{2}$）2016的结果是（ ）
| A． | $\frac{2}{3}$ | B． | $-\frac{2}{3}$ | C． | $\frac{3}{2}$ | D． | $-\frac{3}{2}$ |
7．如果3x3yn+（m-2）x是关于x、y的五次二项式，则m、n的值为（ ）
| A． | m=3，n=2 | B． | m≠2，n=2 | C． | m为任意数，n=2 | D． | m≠2，n=3 |
