题目内容
 如图,已知直线L两侧各有一点A与C,AD⊥L,CB⊥L,AO=5,CB=1,OB=8,OB上有一个动点P,设OP=x.
如图,已知直线L两侧各有一点A与C,AD⊥L,CB⊥L,AO=5,CB=1,OB=8,OB上有一个动点P,设OP=x.(1)请用含x的式子表示AP+PC的长;
(2)请问当P满足什么条件时,AP+PC的值最小,并求出其最小值是多少?
考点:轴对称-最短路线问题
专题:
分析:(1)表示出BP,再利用勾股定理列式即可得解;
(2)根据两点之间线段最短判断出A、P、C三点共线时AP+PC的值最小,然后利用勾股定理列式计算即可得解.
(2)根据两点之间线段最短判断出A、P、C三点共线时AP+PC的值最小,然后利用勾股定理列式计算即可得解.
解答: 解:(1)∵OP=x,OB=8,
解:(1)∵OP=x,OB=8,
∴BP=8-x,
由勾股定理得,AP=
=
,
PC=
=
,
∴AP+PC=
+
;
(2)由两点之间线段最短可知,点P在直线AC与直线L的交点上时,AP+PC的值最小,
最小值=
=10.
 解:(1)∵OP=x,OB=8,
解:(1)∵OP=x,OB=8,∴BP=8-x,
由勾股定理得,AP=
| AO2+OP2 |
| x2+25 |
PC=
| BP2+BC2 |
| (8-x)2+1 |
∴AP+PC=
| x2+25 |
| (8-x)2+1 |
(2)由两点之间线段最短可知,点P在直线AC与直线L的交点上时,AP+PC的值最小,
最小值=
| (5+1)2+82 |
点评:本题考查了勾股定理,轴对称确定最短路线问题,两点之间线段最短的性质,难点在于(2)判断出点P的位置并确定用勾股定理列式求解.

练习册系列答案
相关题目
 如图,△ABC中,AD⊥BC,垂足为D,DE平分∠ADB,交AB于E,∠C=∠DAC,DE与CA平行吗?为什么?
如图,△ABC中,AD⊥BC,垂足为D,DE平分∠ADB,交AB于E,∠C=∠DAC,DE与CA平行吗?为什么?
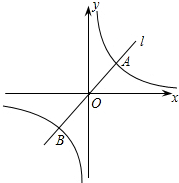 我们知道,y=x的图象向右平移1个单位得到y=x-1的图象,类似的,y=
我们知道,y=x的图象向右平移1个单位得到y=x-1的图象,类似的,y=
 如图,?ABCD中,点E在CD的延长线上,AE∥BD,EC=4,则AB的长是
如图,?ABCD中,点E在CD的延长线上,AE∥BD,EC=4,则AB的长是