题目内容
7.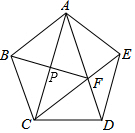 如图,正五边形ABCDE中,连接AC、AD、CE,CE交AD于点F,连接BF,BF与AC交于点P.
如图,正五边形ABCDE中,连接AC、AD、CE,CE交AD于点F,连接BF,BF与AC交于点P.(1)求证:四边形ABCF是菱形;
(2)求证:AC2+BF2=4AB2;
(3)若AB=2,求△CDF的周长.
分析 (1)根据正多边形的内角和定理求出内角的度数,根据菱形的判定定理证明;
(2)根据菱形的对角线互相垂直、勾股定理证明;
(3)根据正五边形的性质、黄金分割的概念计算即可.
解答 (1)证明:正五边形的内角的度数为:$\frac{(n-2)×180°}{5}$=108°,
∵DE=DC,
∴∠DEC=36°,
∴∠AEC=72°,
∴∠BAE+∠AEC=180°,
∴AB∥CF,
同理,BC∥AF,
∴四边形ABCF是平行四边形,
∵BA=BC,
∴四边形ABCF是菱形;
(2)证明:四边形ABCF是菱形,
∴AC⊥BF,
由勾股定理得PB2+PC2=BC2,
∴AC2+BF2=(2PC)2+(2PB)2=4PC2+4PB2=4BC2,
∴AC2+BF2=4AB2;
(3)解:∵四边形ABCF是菱形,
∴CF=AF,
∴△CDF的周长等于CF+DF+CD,
即△CDF的周长等于AD+CD,
∵在正五边形ABCDE中,
∴CD2=DF•DA,即AD•(AD-2)=4,
整理得,AD2-2AD-4=0,
解得,AD=$\sqrt{5}$+1,
∴△CDF的周长等于$\sqrt{5}$+3.
点评 本题考查的是正多边形与圆,掌握正多边形的性质、黄金分割的概念、勾股定理的应用是解题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
18.在下列给出的各数中,最小的一个是( )
| A. | -2 | B. | $-\sqrt{5}$ | C. | 0 | D. | 1 |
12.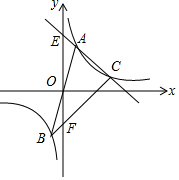 如图,已知直线y=3x与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,其中A(1,3),点C是反比例函数在第一象限的图象上不同于A的一点,直线AC交y轴于点E,直线BC交y轴于点F,则线段EF的长是( )
如图,已知直线y=3x与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,其中A(1,3),点C是反比例函数在第一象限的图象上不同于A的一点,直线AC交y轴于点E,直线BC交y轴于点F,则线段EF的长是( )
 如图,已知直线y=3x与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,其中A(1,3),点C是反比例函数在第一象限的图象上不同于A的一点,直线AC交y轴于点E,直线BC交y轴于点F,则线段EF的长是( )
如图,已知直线y=3x与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,其中A(1,3),点C是反比例函数在第一象限的图象上不同于A的一点,直线AC交y轴于点E,直线BC交y轴于点F,则线段EF的长是( )| A. | 4 | B. | 5 | C. | 6 | D. | 变量 |
16.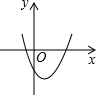 二次函数y=ax2+bx+c的图象如图所示,下列结论错误的是( )
二次函数y=ax2+bx+c的图象如图所示,下列结论错误的是( )
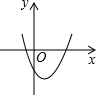 二次函数y=ax2+bx+c的图象如图所示,下列结论错误的是( )
二次函数y=ax2+bx+c的图象如图所示,下列结论错误的是( )| A. | a>0 | B. | b>0 | C. | c<0 | D. | ac<0 |
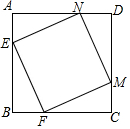 如图,E、F、M、A分别是正方形ABCD四条边上的点,且AE=BF=CM=DN.求证:四边形EFMN是正方形.
如图,E、F、M、A分别是正方形ABCD四条边上的点,且AE=BF=CM=DN.求证:四边形EFMN是正方形.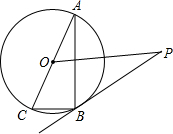 已知:如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点,∠PBA=∠C.
已知:如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点,∠PBA=∠C.