题目内容
4. (1)解不等式组:$\left\{\begin{array}{l}{3x+1≤2}\\{\frac{2x-1}{3}>x}\end{array}\right.$
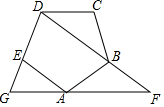
(1)解不等式组:$\left\{\begin{array}{l}{3x+1≤2}\\{\frac{2x-1}{3}>x}\end{array}\right.$(2)如图,已知正五边形ABCDE,AF∥CD交DB的延长线于点F,交DE的延长线于点G.求∠G的度数.
分析 (1)根据不等式的解法即可得到结论;
(2)根据五边形ABCDE是正五边形,得到∠DCB=∠EDC=108°,DC=BC根据等腰三角形的性质得到∠CDB=36°,求得∠GDB=72°,根据平行线的性质即可得到结论.
解答 解:(1)$\left\{\begin{array}{l}{3x+1≤2①}\\{\frac{2x-1}{3}>x②}\end{array}\right.$,
解不等式①,得x≤2,解不等式②,得x<-1,
不等式组的解集为x<-1;
(2)∵五边形ABCDE是正五边形,
∴∠DCB=∠EDC=108°,DC=BC,
∴∠CDB=36°,
∴∠GDB=72°,
∵AF∥CD,
∴∠CDB=∠F=36°,
∴∠G=72°.
点评 本题考查了不等式的解法,多边形的内角和外角,平行线的性质,正确的识别图形是解题的关键.

练习册系列答案
相关题目
1.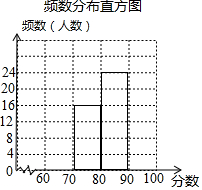 九 (1)班48名学生参加学校举行的“珍惜生命,远离毒品”只是竞赛初赛,赛后,班长对成绩进行分析,制作如下的频数分布表和频数分布直方图(未完成).余下8名学生成绩尚未统计,这8名学生成绩如下:60,90,63,99,67,99,99,68.
九 (1)班48名学生参加学校举行的“珍惜生命,远离毒品”只是竞赛初赛,赛后,班长对成绩进行分析,制作如下的频数分布表和频数分布直方图(未完成).余下8名学生成绩尚未统计,这8名学生成绩如下:60,90,63,99,67,99,99,68.
频数分布表
请解答下列问题:
(1)完成频数分布表,a=4,b=4.
(2)补全频数分布直方图;
(3)全校共有600名学生参加初赛,估计该校成绩90≤x<100范围内的学生有多少人?
(4)九 (1)班甲、乙、丙三位同学的成绩并列第一,现选两人参加决赛,求恰好选中甲、乙两位同学的概率.
 九 (1)班48名学生参加学校举行的“珍惜生命,远离毒品”只是竞赛初赛,赛后,班长对成绩进行分析,制作如下的频数分布表和频数分布直方图(未完成).余下8名学生成绩尚未统计,这8名学生成绩如下:60,90,63,99,67,99,99,68.
九 (1)班48名学生参加学校举行的“珍惜生命,远离毒品”只是竞赛初赛,赛后,班长对成绩进行分析,制作如下的频数分布表和频数分布直方图(未完成).余下8名学生成绩尚未统计,这8名学生成绩如下:60,90,63,99,67,99,99,68.频数分布表
| 分数段 | 频数(人数) |
| 60≤x<70 | a |
| 70≤x<80 | 16 |
| 80≤x<90 | 24 |
| 90≤x<100 | b |
(1)完成频数分布表,a=4,b=4.
(2)补全频数分布直方图;
(3)全校共有600名学生参加初赛,估计该校成绩90≤x<100范围内的学生有多少人?
(4)九 (1)班甲、乙、丙三位同学的成绩并列第一,现选两人参加决赛,求恰好选中甲、乙两位同学的概率.
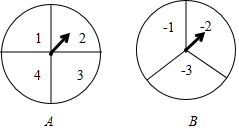 爸爸下班回家呆了一张同事送的《加勒比海盗5》的电影票,结果两小儿子都想要去看,于是爸爸提议用如图所示的两个转盘(其中转盘A被等分成4个扇形,且4个扇形内依次标有数字:1,2,3,4;转盘B被等分成3个扇形,且3个扇形内依次标有数字:-1,-2,-3)做游戏来决定谁去.
爸爸下班回家呆了一张同事送的《加勒比海盗5》的电影票,结果两小儿子都想要去看,于是爸爸提议用如图所示的两个转盘(其中转盘A被等分成4个扇形,且4个扇形内依次标有数字:1,2,3,4;转盘B被等分成3个扇形,且3个扇形内依次标有数字:-1,-2,-3)做游戏来决定谁去.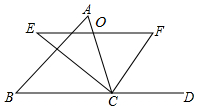 如图,在△ABC中,点O是边AC上一个动点,过点O作直线EF∥BC分别交∠ACB、外角∠ACD的平分线于点E、F.
如图,在△ABC中,点O是边AC上一个动点,过点O作直线EF∥BC分别交∠ACB、外角∠ACD的平分线于点E、F.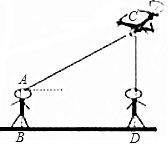 我区中小学生广播操比赛中,无人机对此次比赛的全过程进行了航拍,如图,某一时刻,无人机刚好飞至小琪头顶上方,而站在离小琪35米远的小珺仰望无人机,仰角为36°,已知小珺的眼睛离地面的距离AB为1.63m,那么此时无人机离地面大约有多高?(结果精确到0.1m)(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73)
我区中小学生广播操比赛中,无人机对此次比赛的全过程进行了航拍,如图,某一时刻,无人机刚好飞至小琪头顶上方,而站在离小琪35米远的小珺仰望无人机,仰角为36°,已知小珺的眼睛离地面的距离AB为1.63m,那么此时无人机离地面大约有多高?(结果精确到0.1m)(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73)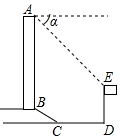 如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公楼顶端A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1:$\sqrt{3}$,求大楼AB的高度是多少?(精确到0.1米,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,$\sqrt{6}$≈2.45)
如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公楼顶端A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1:$\sqrt{3}$,求大楼AB的高度是多少?(精确到0.1米,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,$\sqrt{6}$≈2.45)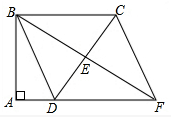 如图,四边形ABCD中,∠A=∠ABC=90°,AD=1,BC=3,E是边CD的中点,连接BE并延长与AD的延长线相交于点F.
如图,四边形ABCD中,∠A=∠ABC=90°,AD=1,BC=3,E是边CD的中点,连接BE并延长与AD的延长线相交于点F.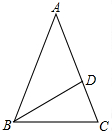 如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D.
如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D.