题目内容
13．
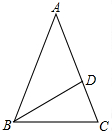如图，在△ABC中，AB=AC，∠A=36°，BD平分∠ABC交AC于点D．求证：AD=BC．
分析 根据等腰三角形的性质得到∠ABC=C=72°，根据角平分线的定义得到∠ABD=∠DBC=36°，∠BDC=72°，根据等腰三角形的判定即可得到结论．
解答 证明：∵AB=AC，∠A=36°，
∴∠ABC=∠C=72°，
∵BD平分∠ABC交AC于点D，
∴∠ABD=∠DBC=36°，∠BDC=72°，
∴∠A=∠ABD，∠BDC=∠C，
∴AD=BD=BC．
点评 本题主要考查等腰三角形的性质和判定，掌握等边对等角是解题的关键，注意三角形内角和定理的应用．
练习册系列答案
一线名师权威作业本系列答案
相关题目
9．
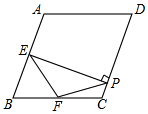如图，在菱形ABCD中，∠A=100°，E，F分别是边AB和BC的中点，EP⊥CD于点P，则∠FPC的度数为（ ）
如图，在菱形ABCD中，∠A=100°，E，F分别是边AB和BC的中点，EP⊥CD于点P，则∠FPC的度数为（ ）| A． | 50° | B． | 55° | C． | 60° | D． | 45° |
（1）解不等式组：$\left\{\begin{array}{l}{3x+1≤2}\\{\frac{2x-1}{3}＞x}\end{array}\right.$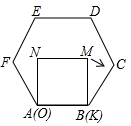
已知正方形MNOK和正六边形ABCDEF边长均为1，把正方形放在正六边形中，使OK边与AB边重合，如图所示，按下列步骤操作：
已知△ABC中，∠ABC=∠ACB，点D，E分别为边AB、AC的中点，求证：BE=CD．
在2017年的理化生实验考试中某校6名学生的实验成绩统计如图，这组数据的众数是26分．