题目内容
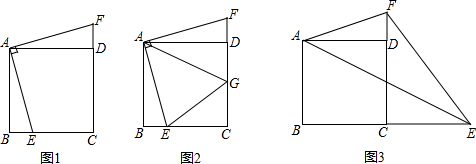
如图1,已知正方形ABCD,把一个直角与正方形叠合,使直角顶点与一重合,当直角的一边与BC相交于E点,另一边与CD的延长线相交于F点时.
(1)证明:BE=DF;
(2)如图2,作∠EAF的平分线交CD于G点,连接EG.证明:BE+DG=EG;
(3)如图3,将图1中的“直角”改为“∠EAF=45°”,当∠EAF的一边与BC的延长线相交于E点,另一边与CD的延长线相交于F点,连接EF.线段BE,DF和EF之间有怎样的数量关系?并加以证明.
(1)证明:BE=DF;
(2)如图2,作∠EAF的平分线交CD于G点,连接EG.证明:BE+DG=EG;
(3)如图3,将图1中的“直角”改为“∠EAF=45°”,当∠EAF的一边与BC的延长线相交于E点,另一边与CD的延长线相交于F点,连接EF.线段BE,DF和EF之间有怎样的数量关系?并加以证明.

考点:四边形综合题
专题:综合题
分析:(1)根据正方形的性质得AB=AD,∠BAD=∠B=∠ADC=90°,再根据等角的余角相等得∠BAE=∠DAF,则可根据“ASA”证明△ABE≌△ADF,然后根据全等的性质即可得到BE=DF;
(2)由△ABE≌△ADF得AE=AF,再根据角平分线的定义得∠EAG=∠FAG,然后根据“SAS”可判断△AEG≌△FAG,得到GE=GF,由于GF=DG+DF,所以BE+DG=EG;
(3)作AG⊥AF交BC于G点,如图3,与(1)一样可证明△ABG≌△ADF,得到BG=DF,AG=AF;再与(2)一样可证明△AEG≌△AEF得到EF=EG,利用BE=BG+GE,
即可得到BE=DF+EF.
(2)由△ABE≌△ADF得AE=AF,再根据角平分线的定义得∠EAG=∠FAG,然后根据“SAS”可判断△AEG≌△FAG,得到GE=GF,由于GF=DG+DF,所以BE+DG=EG;
(3)作AG⊥AF交BC于G点,如图3,与(1)一样可证明△ABG≌△ADF,得到BG=DF,AG=AF;再与(2)一样可证明△AEG≌△AEF得到EF=EG,利用BE=BG+GE,
即可得到BE=DF+EF.
解答:(1)证明:∵四边形ABCD为正方形,
∴AB=AD,∠BAD=∠B=∠ADC=90°,
∵∠EAF=90°,即∠EAD+∠FAD=90°,
而∠EAD+∠BAE=90°,
∴∠BAE=∠DAF,
在△ABE和△ADF中,
,
∴△ABE≌△ADF(ASA),
∴BE=DF;
(2)证明:∵△ABE≌△ADF,
∴AE=AF,
∵∠EAF的平分线交CD于G点,
∴∠EAG=∠FAG,
在△AEG和△FAG中
,
∴△AEG≌△FAG(SAS),
∴GE=GF,
∵GF=DG+DF,
而BE=DF,
∴BE+DG=EG;
(3)解:BE=DF+EF.理由如下:
作AG⊥AF交BC于G点,如图3,
与(1)一样可证明△ABG≌△ADF,
∴BG=DF,AG=AF,
∵∠EAF=45°,
∴∠EAG=90°-∠EAF=45°,
与(2)一样可证明△AEG≌△AEF,
∴EF=EG,
∵BE=BG+GE,
∴BE=DF+EF.
∴AB=AD,∠BAD=∠B=∠ADC=90°,
∵∠EAF=90°,即∠EAD+∠FAD=90°,
而∠EAD+∠BAE=90°,
∴∠BAE=∠DAF,
在△ABE和△ADF中,
|
∴△ABE≌△ADF(ASA),
∴BE=DF;
(2)证明:∵△ABE≌△ADF,
∴AE=AF,
∵∠EAF的平分线交CD于G点,
∴∠EAG=∠FAG,
在△AEG和△FAG中
|
∴△AEG≌△FAG(SAS),

∴GE=GF,
∵GF=DG+DF,
而BE=DF,
∴BE+DG=EG;
(3)解:BE=DF+EF.理由如下:
作AG⊥AF交BC于G点,如图3,
与(1)一样可证明△ABG≌△ADF,
∴BG=DF,AG=AF,
∵∠EAF=45°,
∴∠EAG=90°-∠EAF=45°,
与(2)一样可证明△AEG≌△AEF,
∴EF=EG,
∵BE=BG+GE,
∴BE=DF+EF.
点评:本题考查了四边形的综合题:熟练掌握正方形的性质和三角形全等的判定与性质;会运用三角形全等的知识解决线段相等的问题.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
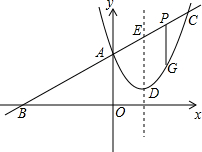 如图,已知二次函数图象的顶点坐标为D(1,1),直线y=kx+m的图象与该二次函数的图象交于A、C两点,且A(0,2),直线与x轴的交点为B,满足
如图,已知二次函数图象的顶点坐标为D(1,1),直线y=kx+m的图象与该二次函数的图象交于A、C两点,且A(0,2),直线与x轴的交点为B,满足 已知AB=AC,AD=AE,AB⊥AC,AD⊥AE.求证:
已知AB=AC,AD=AE,AB⊥AC,AD⊥AE.求证: