题目内容
 点O是△ABC所在平面内一动点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,如果DEFG能构成四边形.
点O是△ABC所在平面内一动点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,如果DEFG能构成四边形.(1)如图,当点O在△ABC的内部时,求证:四边形DEFG是平行四边形;
(2)当点O移动到△ABC的外部时,(1)中的结论是否还成立?画出图形并说明理由;
(3)如果要使四边形DEFG为矩形,那么点O的位置应在
考点:中点四边形
专题:
分析:(1)(2)根据平行四边形的判定性质求证.
(3)把结论当做已知条件,由结论推出已知.
(3)把结论当做已知条件,由结论推出已知.
解答: (1)证明:∵AB、OB、OC、AC中点分别为D、E、F、G
(1)证明:∵AB、OB、OC、AC中点分别为D、E、F、G
∴DG、EF分别为△ABC和△OBC的中位线
∴DG∥BC EF∥BC DG=
BC EF=
BC
∴DG∥EF且DG=EF
∴四边形DEFG是平行四边形;
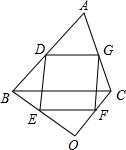 (2)解:成立,
(2)解:成立,
理由是:如图所示,
∵由(1)知,DG∥BC EF∥BC DG=
BC EF=
BC
∴DG∥EF且DG=EF
∴四边形DEFG是平行四边形;
(3)解:当点O满足OA⊥BC,四边形DEFG是矩形.
由三角形中位线性质得∠EDG=90°,
所以平行四边形DEFG是矩形.
故答案是:点O满足OA⊥BC,四边形DEFG是矩形
 (1)证明:∵AB、OB、OC、AC中点分别为D、E、F、G
(1)证明:∵AB、OB、OC、AC中点分别为D、E、F、G∴DG、EF分别为△ABC和△OBC的中位线
∴DG∥BC EF∥BC DG=
| 1 |
| 2 |
| 1 |
| 2 |
∴DG∥EF且DG=EF
∴四边形DEFG是平行四边形;
 (2)解:成立,
(2)解:成立,理由是:如图所示,
∵由(1)知,DG∥BC EF∥BC DG=
| 1 |
| 2 |
| 1 |
| 2 |
∴DG∥EF且DG=EF
∴四边形DEFG是平行四边形;
(3)解:当点O满足OA⊥BC,四边形DEFG是矩形.
由三角形中位线性质得∠EDG=90°,
所以平行四边形DEFG是矩形.
故答案是:点O满足OA⊥BC,四边形DEFG是矩形
点评:本题考查了中点四边形.矩形的判别方法是说明一个四边形为矩形的理论依据,常用三种方法:
①定义;
②三个角是直角相等;
③对角线相等且互相平分.
①定义;
②三个角是直角相等;
③对角线相等且互相平分.

练习册系列答案
相关题目
下列方程中,一定有实数解的是( )
| A、x2+1=0 | ||
| B、(2x+1)2=0 | ||
| C、(2x+1)2+3=0 | ||
D、(
|
 如图,△ABC中,∠A=50°,∠ABC的平分线与∠C的外角∠ACE平分线交于D,求∠D的度数.
如图,△ABC中,∠A=50°,∠ABC的平分线与∠C的外角∠ACE平分线交于D,求∠D的度数. 某市对全市6000名初三学生进行了一次视力抽样调查,绘制出下面的频数分布表和频数分布直方图
某市对全市6000名初三学生进行了一次视力抽样调查,绘制出下面的频数分布表和频数分布直方图 某种洗衣机在洗涤衣服时,经历了进水、清洗、排水、脱水四个连续的过程,其中进水、清洗、排水时洗衣机中的水量y(升)与时间x(分钟)之间的关系如折线图. 根据图象解答下列问题:
某种洗衣机在洗涤衣服时,经历了进水、清洗、排水、脱水四个连续的过程,其中进水、清洗、排水时洗衣机中的水量y(升)与时间x(分钟)之间的关系如折线图. 根据图象解答下列问题: 如图,△ABC中,AB=AC,AD是BC边上中线,那么AD是BC边上高吗?
如图,△ABC中,AB=AC,AD是BC边上中线,那么AD是BC边上高吗?