题目内容
13.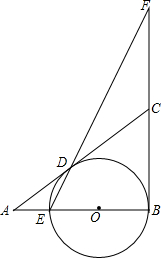 如图,在△ABC中,∠B=90°,O是AB上一点,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D,连结ED,且延长交BC的延长线于点F.
如图,在△ABC中,∠B=90°,O是AB上一点,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D,连结ED,且延长交BC的延长线于点F.(1)求证:BC=FC
(2)若AE:EB=1:3,CD=6,求AD的长.
分析 (1)首先连接BD,由等角的余角相等,易证得∠F=∠EBD.由弦切角定理,易证得∠F=∠CDF.可得CD=CF,又由切线长定理,可得CD=CB,继而可证得BC=FC;
(2)由AE:EB=1:3,设AE=2x,则EB=6x,OE=OD=3x,在Rt△ADO中由勾股定理得AD=4x,再由锐角三角形函数列方程求得.
解答  (1)证明:连接OD,BD、因为AC与⊙O切于点D,则OD⊥AC,
(1)证明:连接OD,BD、因为AC与⊙O切于点D,则OD⊥AC,
∴∠ODC=∠OBC=90°,
又∵OD=OB,
∴∠ODB=∠OBD,
∴∠BDC=∠CBD,
∴DC=BC,
∵BE是直径,
∴∠BDF=∠BDC+∠FDC=90°,
又∵∠CBD+∠F=90°,
∴∠F=∠FDC,
∴DC=CF,
又∵由上面证明可知DC=BC,
∴CF=BC;
(2)解:AE:EB=1:3,
设AE=2x,
则EB=6x,OE=OD=3x,
在Rt△ADO中由勾股定理得AD=4x,
∵tanA=$\frac{OD}{AD}$=$\frac{3x}{4x}$=$\frac{3}{4}$,tanA=$\frac{BC}{AB}$=$\frac{6}{8x}$,
∴x=4,
∴AD=4.
点评 此题考查了切线的性质、相似三角形的判定与性质、弦切角定理、切线长定理以及等腰三角形的判定与性质.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
相关题目
5.在函数y=$\frac{1}{\sqrt{x+1}}$中,自变量x的取值范围是( )
| A. | x≠1 | B. | x≥1 | C. | x>1 | D. | x>-1 |
3.有六根细木条,它们的长度分别为3、8、12、15、17、18(单位:cm),从中取出三根首尾顺次连结搭成一个直角三角形,则这三根细木条的长度分别为( )
| A. | 3,8,12 | B. | 8,15,17 | C. | 12,15,18 | D. | 3,17,18 |
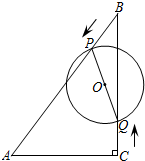 如图,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0≤t≤2),连接PQ,以PQ为直径作⊙O.
如图,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0≤t≤2),连接PQ,以PQ为直径作⊙O.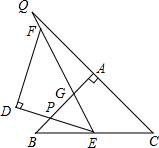 如图,△ABC和△DEF是两个全等的等腰直角三角形,∠BAC=∠EDF=90°,△DEF的顶点E与△ABC的斜边BC的中点重合.将△DEF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,射线EF与线段AB相交于点G,与射线CA相交于点Q.若AQ=12,BP=3,则PG=5.
如图,△ABC和△DEF是两个全等的等腰直角三角形,∠BAC=∠EDF=90°,△DEF的顶点E与△ABC的斜边BC的中点重合.将△DEF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,射线EF与线段AB相交于点G,与射线CA相交于点Q.若AQ=12,BP=3,则PG=5. 如图,菱形OABC的顶点O在坐标原点,顶点B在x轴的正半轴上,OA边所在直线为y=$\frac{\sqrt{3}}{3}$x,AB边所在直线为y=-$\frac{\sqrt{3}}{3}$x+2.
如图,菱形OABC的顶点O在坐标原点,顶点B在x轴的正半轴上,OA边所在直线为y=$\frac{\sqrt{3}}{3}$x,AB边所在直线为y=-$\frac{\sqrt{3}}{3}$x+2.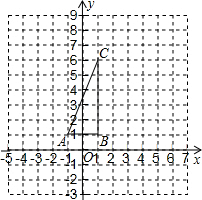 如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-1,1),B(1,1),C(1,6).
如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-1,1),B(1,1),C(1,6).