题目内容
5．在函数y=$\frac{1}{\sqrt{x+1}}$中，自变量x的取值范围是（ ）| A． | x≠1 | B． | x≥1 | C． | x＞1 | D． | x＞-1 |
分析 根据二次根式的性质和分式的意义，被开方数大于或等于0，分母不等于0，可以求出x的范围．
解答 解：根据题意得：x+1≥0且x+1≠0，
解得：x≥-1且x≠-1．
故选D．
点评 本题考查了函数自变量的取值范围问题，函数自变量的范围一般从三个方面考虑：
（1）当函数表达式是整式时，自变量可取全体实数；
（2）当函数表达式是分式时，考虑分式的分母不能为0；
（3）当函数表达式是二次根式时，被开方数非负．
练习册系列答案
相关题目
15．下列几何体中左视图是矩形的共有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
16．某班的9名学生的体重分别是（单位：千克）：70，67，65，63，61，59，59，57，59，这组数据的众数和中位数是（ ）
| A． | 59，61 | B． | 59，63 | C． | 59，65 | D． | 57，61 |
10．
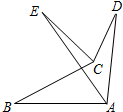如图，∠ABC＞∠ADC，且∠BAD的平分线AE与∠BCD的平分线CE交于点E，则∠AEC与∠ADC、∠ABC之间存在的等量关系是（ ）
如图，∠ABC＞∠ADC，且∠BAD的平分线AE与∠BCD的平分线CE交于点E，则∠AEC与∠ADC、∠ABC之间存在的等量关系是（ ）| A． | ∠AEC=∠ABC-2∠ADC | B． | ∠AEC=$\frac{∠ABC-∠ADC}{2}$ | ||
| C． | ∠AEC=$\frac{1}{2}$∠ABC-∠ADC | D． | ∠AEC=$\frac{∠ABC-∠ADC}{3}$ |
如图，AB是⊙O的直径，C是弧AB的中点，连接AC并延长至D，使DC=CA，连接DB，点E为OB的中点，连接CE并延长交DB的延长线于点F，连接AF交⊙O于点H，连接BH．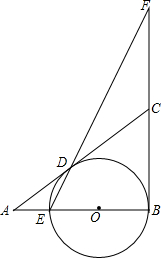
如图，在△ABC中，∠B=90°，O是AB上一点，以O为圆心，OB为半径的圆与AB交于点E，与AC切于点D，连结ED，且延长交BC的延长线于点F．