题目内容
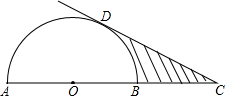 如图,AB是半圆O的直径,延长OB至点C,使BC=AO,过点C作半圆的切线,切点为D.如果半圆的半径为r,图中阴影部分的面积为S,则S可用r表示为
如图,AB是半圆O的直径,延长OB至点C,使BC=AO,过点C作半圆的切线,切点为D.如果半圆的半径为r,图中阴影部分的面积为S,则S可用r表示为考点:切线的性质,扇形面积的计算
专题:
分析:首先连接OD,易得△OCD是直角三角形,且∠C=30°,则可求得CD的长,然后由S=S△OCD-S扇形BOD,求得答案.
解答: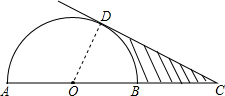 解:连接OD,
解:连接OD,
∵CD是半圆的切线,
∴OD⊥CD,
即∠CDO=90°,
∵BC=AO,AO=BO=DO,
∴OC=2DO=2r,
∴∠C=30°,
∴∠COD=60°,CD=
=
r,
∴S=S△OCD-S扇形BOD=
×r×
r-
=(
-
)r2.
故答案为:(
-
)r2.
 解:连接OD,
解:连接OD,∵CD是半圆的切线,
∴OD⊥CD,
即∠CDO=90°,
∵BC=AO,AO=BO=DO,
∴OC=2DO=2r,
∴∠C=30°,
∴∠COD=60°,CD=
| OC2-OD2 |
| 3 |
∴S=S△OCD-S扇形BOD=
| 1 |
| 2 |
| 3 |
| 60×π×r2 |
| 360 |
| ||
| 2 |
| π |
| 6 |
故答案为:(
| ||
| 2 |
| π |
| 6 |
点评:此题考查了切线的性质以及含30°角的直角三角形的性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
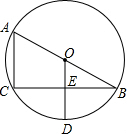 如图,AB是⊙O的直径,BC是弦,OD⊥BC于E,交
如图,AB是⊙O的直径,BC是弦,OD⊥BC于E,交
 如图,AB是⊙O的直径,BC是弦,OD⊥BC于E,交弧BC于D.
如图,AB是⊙O的直径,BC是弦,OD⊥BC于E,交弧BC于D. 根据如图所示的某函数的图象,回答下列问题,
根据如图所示的某函数的图象,回答下列问题, 已知a、b、c在数轴上的位置如图,试求|a+b|+|b|+|-c|的值.
已知a、b、c在数轴上的位置如图,试求|a+b|+|b|+|-c|的值.