题目内容
已知抛物线y=ax2+bx+c,其中a、b为整数,与x轴交于两点,距离为4,对称轴x=-5,则此图形通过下列哪一点: (填字母)
A(-6,-3);B(-6,-4).
A(-6,-3);B(-6,-4).
考点:抛物线与x轴的交点
专题:
分析:根据二次函数图形的对称轴为x=-5,图形与x轴的两个交点距离为4可知两点的坐标为(-7,0)和(-3,0),设出此函数的解析式,把x=-6代入进行计算即可.
解答:解:∵二次函数图形的对称轴为x=-5,图形与x轴的两个交点距离为4,
∴此两点的坐标为(-7,0)和(-3,0).
设二次函数的解析式为:y=(x+7)(x+3),将x=-6代入,得y=(-6+7)(-6+3)=-3
∴点(-6,-3)在二次函数的图象上.
故选:A.
∴此两点的坐标为(-7,0)和(-3,0).
设二次函数的解析式为:y=(x+7)(x+3),将x=-6代入,得y=(-6+7)(-6+3)=-3
∴点(-6,-3)在二次函数的图象上.
故选:A.
点评:本题考查的是抛物线与x轴的交点问题,根据题意得出二次函数的交点式是解答此题的关键.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
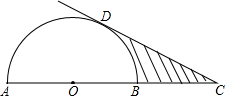 如图,AB是半圆O的直径,延长OB至点C,使BC=AO,过点C作半圆的切线,切点为D.如果半圆的半径为r,图中阴影部分的面积为S,则S可用r表示为
如图,AB是半圆O的直径,延长OB至点C,使BC=AO,过点C作半圆的切线,切点为D.如果半圆的半径为r,图中阴影部分的面积为S,则S可用r表示为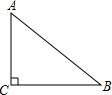 如图,已知Rt△ABC中,∠C=90°,AC=3,BC=4,求AB的长和△ABC的周长.
如图,已知Rt△ABC中,∠C=90°,AC=3,BC=4,求AB的长和△ABC的周长.