题目内容
6.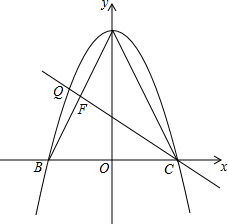 如图,在△ABC中,AB=AC,点A(0,4),B(-2,0),C(2,0),F是AB的中点,以A为顶点的抛物线经过B、C两点且与直线CF交于点Q.
如图,在△ABC中,AB=AC,点A(0,4),B(-2,0),C(2,0),F是AB的中点,以A为顶点的抛物线经过B、C两点且与直线CF交于点Q.(1)求抛物线和直线CF的解析式;
(2)连接BQ,过点A作AM∥x轴交BQ的延长线于点M.求四边形AMQC的面积;
(3)在直线CQ上方的抛物线上有一动点P,当点P移动到什么位置时,△PQC的面积S为最大,最大面积是多少?并求出此时点P坐标.
分析 (1)由题意可设所求抛物线的解析式为y=a(x-2)(x+2),把A点的坐标代入求出a的值即可得到抛物线的解析式;设所求直线的解析式为 y=kx+b,把点F和点C的坐标代入求出k和b的值即可得到直线解析式;
(2)直线CF交抛物线于点Q 可得Q$(-\frac{4}{3},\frac{20}{9})$,设直线BQ的解析式为y=k1x+b1,进而可求出点M的坐标,再根据S四边形AMQC=S梯形AMBC-S△BQC=$\frac{1}{2}$(AM+BC)×AO-$\frac{1}{2}$BC×QE计算即可;
(3)假设△PQC的面积最大时P(x,-x2+4),过点P作PH⊥X轴于H交QC于点D,则D(x,-$\frac{2}{3}$x+$\frac{4}{3}$),由S=S△PQD+S△PDC可得S和x的二次函数关系,利用函数的性质即可求出面积的最大值以及点P的坐标.
解答 解:(1)设所求抛物线的解析式为y=a(x-2)(x+2),
∵抛物线过点A(0,4),
∴a=-1,
∴所求抛物线的解析式为 y=-x2+4,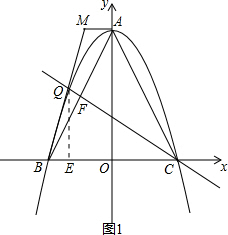
设所求直线的解析式为 y=kx+b,
∵F是线段AB的中点,
∴F(-1,2),
∴$\left\{\begin{array}{l}-k+b=2\\ 2k+b=0\end{array}\right.$
解得:$k=-\frac{2}{3},b=\frac{4}{3}$,
所求直线的解析式为 $y=-\frac{2}{3}x+\frac{4}{3}$,
(2)直线CF交抛物线于点Q 可得Q$(-\frac{4}{3},\frac{20}{9})$,
设直线BQ的解析式为y=k1x+b1
∴$\left\{\begin{array}{l}-\frac{4}{3}{k_1}+{b_1}=\frac{20}{9}\\-2{k_1}+{b_1}=0\end{array}\right.$,
解得:${k_1}=\frac{10}{3},{b_1}=\frac{20}{3}$,
∴直线BQ的解析式为$y=\frac{10}{3}x+\frac{20}{3}$,
∵直线AM∥X轴 M的纵坐标为4 可得M$(-\frac{4}{5},4)$,
∴AM=$\frac{4}{5}$,
过Q作QE⊥X轴于E则QE=$\frac{20}{9}$,
∴S四边形AMQC=S梯形AMBC-S△BQC=$\frac{1}{2}$(AM+BC)×AO-$\frac{1}{2}$BC×QE,
=$\frac{1}{2}(\frac{4}{5}+4)×4-\frac{1}{2}×4×\frac{20}{9}=\frac{232}{45}$(平方单位)
(3)假设△PQC的面积最大时P(x,-x2+4),过点P作PH⊥X轴于H交QC于 点D,则D(x,-$\frac{2}{3}$x+$\frac{4}{3}$),
点D,则D(x,-$\frac{2}{3}$x+$\frac{4}{3}$),
∵PD=PH-DH=$-{x^2}+4-(-\frac{2}{3}x+\frac{4}{3})$=$-{x^2}+\frac{2}{3}x+\frac{8}{3}$,
S=S△PQD+S△PDC,
=$\frac{1}{2}$DP×NH+$\frac{1}{2}$DP×HC=$\frac{1}{2}$DP(NH+HC),
=$\frac{1}{2}DP×(2+\frac{4}{3})$=$\frac{1}{2}(-{x^2}+\frac{2}{3}x+\frac{8}{3})×\frac{10}{3}$,
=$-\frac{5}{3}{x^2}+\frac{10}{9}x+\frac{40}{9}$
=$-\frac{5}{3}{(x-\frac{1}{3})^2}+\frac{125}{27}$,
∵$a=-\frac{3}{5}<0$,
∴S有最大值$\frac{125}{27}$,
∴P$(\frac{1}{3},\frac{35}{9})$.
点评 本题主要考查了二次函数与方程、几何知识的综合应用,解题的关键是将函数问题转化为方程问题,善于利用几何图形的有关性质、定理和二次函数的知识求解.

 如图,BD是⊙O的直径,弦AC⊥BD,垂足为E,∠AOB=60°,则∠BDC等于( )
如图,BD是⊙O的直径,弦AC⊥BD,垂足为E,∠AOB=60°,则∠BDC等于( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
| 4.7 | 2.0 | 3.1 | 2.3 | 5.2 | 2.8 | 7.3 | 4.3 | 4.8 | 6.7 |
| 4.5 | 5.1 | 6.5 | 8.9 | 2.0 | 4.5 | 3.2 | 3.2 | 4.5 | 3.5 |
| 3.5 | 3.5 | 3.6 | 4.9 | 3.7 | 3.8 | 5.6 | 5.5 | 5.9 | 6.2 |
| 5.7 | 3.9 | 4.0 | 4.0 | 7.0 | 3.7 | 8.3 | 4.2 | 6.4 | 3.5 |
| 4.5 | 4.5 | 4.6 | 5.4 | 5.6 | 6.6 | 5.8 | 4.5 | 6.2 | 7.5 |
(2)为了鼓励节约用水,要确定一个用水量的标准,抽出这个标准的部分按1.5倍价格收费,若要使60%的家庭水费支出不受影响,你觉得家庭月均用水量应该定为多少?为什么?
 平行四边形ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为( )
平行四边形ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为( )| A. | 3cm | B. | 6cm | C. | 9cm | D. | 12cm |
 如图,过反比例函数y=$\frac{k}{x}$图象上三点A、B、C分别作直角三角形和矩形,图中S1+S2=5,则S3=5.
如图,过反比例函数y=$\frac{k}{x}$图象上三点A、B、C分别作直角三角形和矩形,图中S1+S2=5,则S3=5.
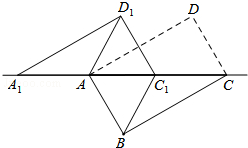 如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连结AD1、BC1.若∠ACB=30°,AB=1,CC1=x,△ACD与△A1C1D1重叠部分的面积为s,则下列结论:
如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连结AD1、BC1.若∠ACB=30°,AB=1,CC1=x,△ACD与△A1C1D1重叠部分的面积为s,则下列结论: