题目内容
13.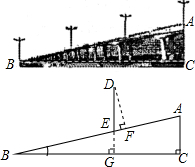 如图是某城市一座立交桥的引桥部分,桥面截面AB可以近似地看做Rt△ABC的斜边,桥面AB上路灯DE的高度为5m,已知坡角∠ABC为14°,求路灯DE的顶端D点到桥面AB的垂直距离(即DF的长,精确到0.1m).
如图是某城市一座立交桥的引桥部分,桥面截面AB可以近似地看做Rt△ABC的斜边,桥面AB上路灯DE的高度为5m,已知坡角∠ABC为14°,求路灯DE的顶端D点到桥面AB的垂直距离(即DF的长,精确到0.1m).【参考数据:sin14°=0.24,cos14°=0.97,tan14°=0.25】
分析 首先得到∠EDF=∠ABC=14°,然后在Rt△DEF中利用余弦的定义得到DF=DEcos∠EDF即可.
解答 解:在Rt△BEG和Rt△DEF中,
∵∠BEG=∠DEF,
∴∠EDF=∠ABC=14°,
在Rt△DEF中,
∵cos∠EDF=$\frac{DF}{DE}$,
∴DF=DEcos∠EDF=5×cos14°=5×0.97=4.85≈4.9m.
答:路灯DE的顶端D点到桥面AB的垂直距离为4.9米.
点评 本题考查了解直角三角形的知识,解题的关键是能够从实际问题中整理出直角三角形并选择合适的边角关系求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.某次篮球联赛积分
(1)求胜一场、负一场积分各是多少?
(2)某队胜场总积分能等于它的负场总积分?
| 队名 | 比赛场次 | 胜场 | 负场 | 积分 |
| 前进 | 14 | 10 | 4 | 24 |
| 东方 | 10 | 4 | 4 | 24 |
| 光明 | 14 | 9 | 5 | 23 |
| 蓝天 | 14 | 9 | 5 | 23 |
| 雄鹰 | 14 | 7 | 7 | 21 |
| 远大 | 14 | 7 | 7 | 21 |
| 卫星 | 14 | 4 | 10 | 18 |
(2)某队胜场总积分能等于它的负场总积分?
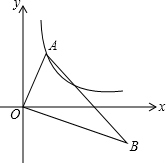 如图,在Rt△AOB中,O为坐标原点,∠AOB=90°,∠B=30°.若点A在反比例函数y=$\frac{2}{x}$(x>0)的图象上运动,点B在反比例函数y=$\frac{k}{x}$(x>O)的图象上运动,则k=-6.
如图,在Rt△AOB中,O为坐标原点,∠AOB=90°,∠B=30°.若点A在反比例函数y=$\frac{2}{x}$(x>0)的图象上运动,点B在反比例函数y=$\frac{k}{x}$(x>O)的图象上运动,则k=-6. 如图,∠BAC=30°,点P是∠BAC平分线上一点,PM∥AC交AB于点M,PD⊥AC于点D,若PD+PM=12,则AM=8.
如图,∠BAC=30°,点P是∠BAC平分线上一点,PM∥AC交AB于点M,PD⊥AC于点D,若PD+PM=12,则AM=8.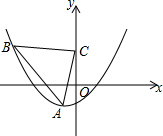 已知,抛物线y=$\frac{1}{8}$(x+1)2-2顶点为A,点B在抛物线上,以AB的斜边作等腰直角三角形,直角顶点C在y轴上,求C点坐标.
已知,抛物线y=$\frac{1}{8}$(x+1)2-2顶点为A,点B在抛物线上,以AB的斜边作等腰直角三角形,直角顶点C在y轴上,求C点坐标.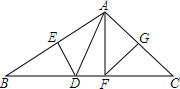 如图,在△ABC中,DE、FG分别为AB、AC的垂直平分线,连接AD、AF.
如图,在△ABC中,DE、FG分别为AB、AC的垂直平分线,连接AD、AF.