题目内容
2.已知实数a、b满足b=$\frac{\sqrt{{a}^{2}-9}+\sqrt{9-{a}^{2}}}{a-3}$+5,则a2+b2的值为34.分析 根据被开方数是非负数,分母不能为零,可得a、b的值,根据有理数的运算,可得答案.
解答 解:由实数a、b满足b=$\frac{\sqrt{{a}^{2}-9}+\sqrt{9-{a}^{2}}}{a-3}$+5,得
$\left\{\begin{array}{l}{{a}^{2}-9≥0}\\{9-{a}^{2}≥0}\\{a-3≠0}\end{array}\right.$,
解得a=-3,b=5.
a2+b2=(-3)2+52=9+25=34,
故答案为:34.
点评 本题考查了二次根式有意义的条件,利用被开方数是非负数,分母不能为零得出a、b的值是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10. 如图,四边形ABCD中,∠A=90°,AB=$3\sqrt{3}$,AD=3,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为( )
如图,四边形ABCD中,∠A=90°,AB=$3\sqrt{3}$,AD=3,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为( )
 如图,四边形ABCD中,∠A=90°,AB=$3\sqrt{3}$,AD=3,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为( )
如图,四边形ABCD中,∠A=90°,AB=$3\sqrt{3}$,AD=3,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为( )| A. | 3 | B. | 4 | C. | 4.5 | D. | 5 |
12. 如果,正方形ABCD的边长为2cm,E为CD边上一点,∠DAE=30°,M为AE的中点,过点M作直线分别与AD、BC相交于点P、Q,若PQ=AE,则PD等于( )
如果,正方形ABCD的边长为2cm,E为CD边上一点,∠DAE=30°,M为AE的中点,过点M作直线分别与AD、BC相交于点P、Q,若PQ=AE,则PD等于( )
 如果,正方形ABCD的边长为2cm,E为CD边上一点,∠DAE=30°,M为AE的中点,过点M作直线分别与AD、BC相交于点P、Q,若PQ=AE,则PD等于( )
如果,正方形ABCD的边长为2cm,E为CD边上一点,∠DAE=30°,M为AE的中点,过点M作直线分别与AD、BC相交于点P、Q,若PQ=AE,则PD等于( )| A. | $\frac{2}{3}$cm或$\frac{2}{3}\sqrt{3}$cm | B. | $\frac{2}{3}\sqrt{3}$cm | C. | $\frac{4}{3}$cm或$\frac{2}{3}\sqrt{3}$cm | D. | $\frac{2}{3}$cm或$\frac{4}{3}$cm |
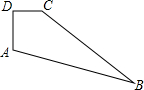 如图,在四边形ABCD中,AD⊥DC,AD=8,DC=6,CB=24,AB=26,则四边形ABCD的面积为144.
如图,在四边形ABCD中,AD⊥DC,AD=8,DC=6,CB=24,AB=26,则四边形ABCD的面积为144.