题目内容
16.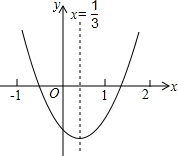 小明从如图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面五条信息:
小明从如图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面五条信息:①c<0;②abc<0;③a-b+c>0;④2a-3b=0;⑤4a+2b+c>0.
你认为其中正确的是( )
| A. | ①②④ | B. | ①③⑤ | C. | ②③⑤ | D. | ①③④⑤ |
分析 由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解答 解:因为函数图象与y轴的交点在y轴的负半轴可知,
所以c<0,∴①正确;
∵函数图象开口向上,
∴a>0,由①知,c<0,
由函数的对称轴在x的正半轴上可知,x=-$\frac{b}{2a}$>0,故b<0,故abc>0,∴②错误;
∵把x=-1代入函数解析式,由函数的图象可知,x=-1时,y>0即a-b+c>0,∴③正确;
∵a>0,b<0,
∴2a>3b,
∴2a-3b>0,∴④错误;
∵把x=2代入函数解析式,由函数的图象可知,x=2时,y>0即4a+2b+c>0,∴⑤正确;
其中正确的有①③⑤,
故选B.
点评 本题考查了图象与二次函数系数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换,根的判别式的熟练运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.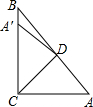 如图,在△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上A′处,折痕为CD,则∠BDA′的度数为( )
如图,在△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上A′处,折痕为CD,则∠BDA′的度数为( )
 如图,在△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上A′处,折痕为CD,则∠BDA′的度数为( )
如图,在△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上A′处,折痕为CD,则∠BDA′的度数为( )| A. | 40° | B. | 30° | C. | 20° | D. | 10° |
11.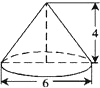 如图,已知圆锥的高为4,底面圆的直径为6,则此圆锥的侧面积是( )
如图,已知圆锥的高为4,底面圆的直径为6,则此圆锥的侧面积是( )
 如图,已知圆锥的高为4,底面圆的直径为6,则此圆锥的侧面积是( )
如图,已知圆锥的高为4,底面圆的直径为6,则此圆锥的侧面积是( )| A. | 12π | B. | 15π | C. | 20π | D. | 30π |
1.下列二次根式是最简二次根式的是( )
| A. | $\sqrt{12}$ | B. | $\sqrt{14}$ | C. | $\sqrt{16}$ | D. | $\sqrt{18}$ |
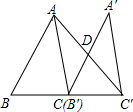 已知:如图,△ABC的面积为12,将△ABC沿BC方向移到△A′B′C′的位置,使B′与C重合,连结AC′交A′C于D,则△C′DC的面积为6.
已知:如图,△ABC的面积为12,将△ABC沿BC方向移到△A′B′C′的位置,使B′与C重合,连结AC′交A′C于D,则△C′DC的面积为6. 如图是一个正方体被截去一个正三棱锥得到的几何体,该几何体的俯视图为( )
如图是一个正方体被截去一个正三棱锥得到的几何体,该几何体的俯视图为( )


