题目内容
1.将边长分别为$\sqrt{2}$、2$\sqrt{2}$、3$\sqrt{2}$、4$\sqrt{2}$、…的正方形的面积分别记作S1,S2,S3,S4…,计算S2-S1,S3-S2,S4-S3….若边长为n$\sqrt{2}$(n为正整数)的正方形面积记作Sn,根据你的计算结果,猜想Sn-Sn-1=4n-2.(用含n的式子表示)分析 首先求出S2-S1,S3-S2,S4-S3,…,得出规律,即可得出Sn-Sn-1.
解答 解:∵S2-S1=(2$\sqrt{2}$)2-($\sqrt{2}$)2=6,
S3-S2=(3$\sqrt{2}$)2-(2$\sqrt{2}$)2=10,
S4-S3=(4$\sqrt{2}$)2-(3$\sqrt{2}$)2=14,…,
∴Sn-Sn-1=(n$\sqrt{2}$)2-[(n-1)$\sqrt{2}$]2=4n-2.
故答案为:4n-2.
点评 此题主要考查了正方形的性质、正方形的面积计算;熟练掌握正方形的性质和面积的计算,发现数据之间的规律是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.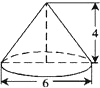 如图,已知圆锥的高为4,底面圆的直径为6,则此圆锥的侧面积是( )
如图,已知圆锥的高为4,底面圆的直径为6,则此圆锥的侧面积是( )
 如图,已知圆锥的高为4,底面圆的直径为6,则此圆锥的侧面积是( )
如图,已知圆锥的高为4,底面圆的直径为6,则此圆锥的侧面积是( )| A. | 12π | B. | 15π | C. | 20π | D. | 30π |
16. 如图,连接正五边形的两条对角线,得到的图形( )
如图,连接正五边形的两条对角线,得到的图形( )
 如图,连接正五边形的两条对角线,得到的图形( )
如图,连接正五边形的两条对角线,得到的图形( )| A. | 既是轴对称图形也是中心对称图形 | |
| B. | 是轴对称图形不是中心对称图形 | |
| C. | 是中心对称图形但不是轴对称图形 | |
| D. | 既不是轴对称图形也不是中心对称图形 |
13.△ABC中,∠A:∠B:∠C=1:1:2,a,b,c分别为∠A,∠B,∠C的对边,则有( )
| A. | b2+c2=a2 | B. | c2=3b2 | C. | 3a2=2c2 | D. | c2=2b2 |
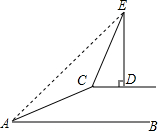 如图,某河大堤上有一棵树ED,ED⊥CD,并且CD与水平地面AB平行,小明在A处测得树顶E的仰角为45°,然后沿着坡度为1:2的斜坡AC攀行20米,在坡顶C处又测得树顶E的仰角为76°,求树ED的高度.(精确到1米)
如图,某河大堤上有一棵树ED,ED⊥CD,并且CD与水平地面AB平行,小明在A处测得树顶E的仰角为45°,然后沿着坡度为1:2的斜坡AC攀行20米,在坡顶C处又测得树顶E的仰角为76°,求树ED的高度.(精确到1米)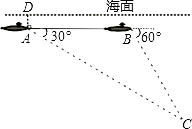 一架空客A320-200型客机2014年12月28日从印尼泗水飞往新加坡途中失事.我国政府马上派出舰船搜救,我海军一艘潜艇在海面下500米A点处测得仰角为30°正前方的海底有疑似黑匣子信号发出,继续在同一深度直线航行3000米后再次在B点处测得俯角为60°正前方的海底有疑似黑匣子信号发出,求海底疑似黑匣子C点处距离海面的深度?(结果保留根号)
一架空客A320-200型客机2014年12月28日从印尼泗水飞往新加坡途中失事.我国政府马上派出舰船搜救,我海军一艘潜艇在海面下500米A点处测得仰角为30°正前方的海底有疑似黑匣子信号发出,继续在同一深度直线航行3000米后再次在B点处测得俯角为60°正前方的海底有疑似黑匣子信号发出,求海底疑似黑匣子C点处距离海面的深度?(结果保留根号)