题目内容
17.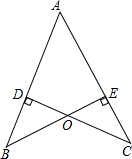 如图CD⊥AB于D,BE⊥AC于E,OD=OE,求证:OB=OC
如图CD⊥AB于D,BE⊥AC于E,OD=OE,求证:OB=OC 证明:
∵CD⊥AB,BE⊥AC
∴∠ODB=∠OEC=90° (垂直的定义)
∵在△BOD和△COE中
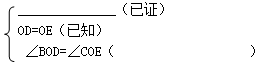
∴△BOD≌△COE(ASA)
∴OB=OC.
分析 只要证明△BOD≌△COE(ASA)即可解决问题.
解答 证明:∵CD⊥AB,BE⊥AC,
∴∠ODB=∠OEC=90°(垂直的定义),
在△BOD和△COE中,
$\left\{\begin{array}{l}{∠ODB=∠COE}\\{OD=OE}\\{∠BOD=∠COE}\end{array}\right.$,
∴△BOD≌△COE(ASA),
∴OB=OC.
故答案为OEC,垂直的定义,ASA,OB=OC.
点评 本题考查全等三角形的判定和性质、解题的关键是熟练掌握基本概念、正确寻找三角形全等的条件,属于中考常考题型.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
7.下列运算正确的是( )
| A. | a+a=a2 | B. | a2•a=a2 | C. | a3÷a2=a (a≠0) | D. | (a2)3=a5 |
8.某水果店有甲、乙两种苹果包装盒,现有360个苹果要用这两种包装盒进行包装,已知每个甲包装盒比每个乙
包装盒少装3个苹果,单独用甲包装盒比单独用乙包装盒多用6个,设每个甲包装盒可装x个苹果,根据题意
下面所列方程正确的是( )
包装盒少装3个苹果,单独用甲包装盒比单独用乙包装盒多用6个,设每个甲包装盒可装x个苹果,根据题意
下面所列方程正确的是( )
| A. | $\frac{360}{x}$=$\frac{360}{x-3}$+6 | B. | $\frac{360}{x}$=$\frac{360}{x+3}$+6 | C. | $\frac{360}{x-3}$=$\frac{360}{x}$+6 | D. | $\frac{360}{x+3}$=$\frac{360}{x}$+6 |
9.下列关于$\sqrt{8}$的说法中,不正确的是( )
| A. | $\sqrt{8}$是无理数 | B. | $\sqrt{8}$的大小介于2和3之间 | ||
| C. | $\sqrt{8}$可以用数轴上的点表示 | D. | $\sqrt{8}$是$\sqrt{2}$的4倍 |
6. 如图,在等腰梯形ABCD中,AC,BD相交于点O,则图中全等三角形的对数有( )
如图,在等腰梯形ABCD中,AC,BD相交于点O,则图中全等三角形的对数有( )
 如图,在等腰梯形ABCD中,AC,BD相交于点O,则图中全等三角形的对数有( )
如图,在等腰梯形ABCD中,AC,BD相交于点O,则图中全等三角形的对数有( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
7.已知关于x的方程2x+m=3的解是x=1,则m的值为( )
| A. | 1 | B. | -1 | C. | 7 | D. | -7 |
 如图,长为10cm的弹性皮筋直放置在直线l上,固定两端A和B,然后把中点C垂直向上拉升12cm至D点,则弹性皮筋被拉长了16cm.
如图,长为10cm的弹性皮筋直放置在直线l上,固定两端A和B,然后把中点C垂直向上拉升12cm至D点,则弹性皮筋被拉长了16cm.