题目内容
18. 6月5日是世界环保日,为了让学生增强环保意识,了解环保知识,某中学政教处举行了一次八年级“环保知识竞赛”,共有900名学生参加了这次活动,为了了解该次竞赛成绩情况,从中抽取了部分学生的成绩(满分100分,得分均为正整数)进行统计,请你根据下面还未完成的频率分布表和频率分布直方图,解答下列问题:
6月5日是世界环保日,为了让学生增强环保意识,了解环保知识,某中学政教处举行了一次八年级“环保知识竞赛”,共有900名学生参加了这次活动,为了了解该次竞赛成绩情况,从中抽取了部分学生的成绩(满分100分,得分均为正整数)进行统计,请你根据下面还未完成的频率分布表和频率分布直方图,解答下列问题:(1)填充频率分布表格中的空格;
| 分组 | 频数 | 频率 |
| 50.5-60.5 | 4 | 0.08 |
| 60.5-70.5 | 8 | 0.16 |
| 70.5-80.5 | 10 | 0.20 |
| 80.5-90.5 | 16 | 0.32 |
| 90.5-100.5 | 12 | 0.24 |
| 合计 |
(3)本题的数据是抽样调查所得,总体是900名学生的成绩,个体是每名学生的成绩,样本容量是50.
(4)若成绩在80分以上(不含80分)为优秀,则该校八年级参赛学生成绩优秀的为504人.
分析 (1)根据第一组的频数是4,对应点频率是0.08即可求得总人数,利用总人数减去其它组的人数求得90.5-100.5一组的频数,根据频率公式求得频率;
(2)根据(1)即可补全直方图;
(3)根据抽样调查的定义以及总体、个体、样本、样本容量的定义求解;
(4)利用总数乘以对应的频率即可求解.
解答 解:(1)调查的总人数是4÷0.08=50(人).
则90.5-100.5一组的人数是50-4-8-10-16=12(人),
对应的频率是$\frac{12}{50}$=0.24.
| 分组 | 频数 | 频率 |
| 50.5-60.5 | 4 | 0.08 |
| 60.5-70.5 | 8 | 0.16 |
| 70.5-80.5 | 10 | 0.20 |
| 80.5-90.5 | 16 | 0.32 |
| 90.5-100.5 | 12 | 0.24 |
| 合计 |
 ;
;(3)数据是抽样调查所得,总体是900名学生的成绩,个体是每名学生的成绩,样本容量是50.
故答案是:抽样、900名学生的成绩、每名学生的成绩,50;
(4)该校八年级参赛学生成绩优秀的人数是900×(0.32+0.24)=504(人).
故答案是:504.
点评 本题考查读频数分布直方图的能力和利用统计图获取信息的能力.利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.

练习册系列答案
相关题目
14. (1)计算:$\sqrt{4}$tan45°$+(\frac{1}{3})^{-1}-2cos60°+(π-2011)^{0}$
(1)计算:$\sqrt{4}$tan45°$+(\frac{1}{3})^{-1}-2cos60°+(π-2011)^{0}$
(2)解方程:x2-4x=3
(3)如果代数式m2-8m-12与5m-42的值相等,求-2m+5的值.
(4)某校数学兴趣小组成员小华对本班上期期末考试数学成绩作了统计分析,绘制成如下频数、频率分布表和频数分布直方图.请你根据图表提供的信息,解答下列问题:
①频数、频率分布表中a=8,b=0.08;
②补全频数分布直方图;
③数学老师准备从不低于90分的学生中选1人介绍学习经验,那么取得了93分的小华
被选上的概率是多少?
 (1)计算:$\sqrt{4}$tan45°$+(\frac{1}{3})^{-1}-2cos60°+(π-2011)^{0}$
(1)计算:$\sqrt{4}$tan45°$+(\frac{1}{3})^{-1}-2cos60°+(π-2011)^{0}$(2)解方程:x2-4x=3
(3)如果代数式m2-8m-12与5m-42的值相等,求-2m+5的值.
(4)某校数学兴趣小组成员小华对本班上期期末考试数学成绩作了统计分析,绘制成如下频数、频率分布表和频数分布直方图.请你根据图表提供的信息,解答下列问题:
①频数、频率分布表中a=8,b=0.08;
②补全频数分布直方图;
③数学老师准备从不低于90分的学生中选1人介绍学习经验,那么取得了93分的小华
被选上的概率是多少?
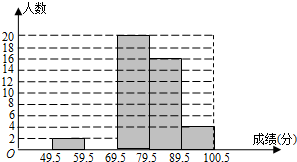
| 分组 | 49.5~59.5 | 59.5~69.5 | 69.5~79.5 | 79.5~89.5 | 89.5~100.5 | 合计 |
| 频数 | 2 | a | 20 | 16 | 4 | 50 |
| 频率 | 0.04 | 0.16 | 0.40 | 0.32 | b | 1 |
 如图,身高为1.6m的某学生想测量一棵大树的高度,她沿着树影BA由B向A走去,当走到C点时,她的影子顶端正好与树的影子顶端A重合,测得BC=9.2m,CA=0.8m,求树的高度BD.
如图,身高为1.6m的某学生想测量一棵大树的高度,她沿着树影BA由B向A走去,当走到C点时,她的影子顶端正好与树的影子顶端A重合,测得BC=9.2m,CA=0.8m,求树的高度BD. 如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:①a>0;②2a+b=0;③a+b+c>0;④△>0;⑤4a-2b+c<0,其中正确的个数为( )
如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:①a>0;②2a+b=0;③a+b+c>0;④△>0;⑤4a-2b+c<0,其中正确的个数为( ) 已知:如图AB∥CD,EF交AB于G,交CD于F,FH平分∠EFD°,交AB与H,∠AGE=50°,求∠BHF的度数.
已知:如图AB∥CD,EF交AB于G,交CD于F,FH平分∠EFD°,交AB与H,∠AGE=50°,求∠BHF的度数.