题目内容
19.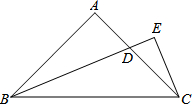 等腰直角三角形ABC中,∠A=90°,∠B的平分线交AC于D,过点C向BD作垂线,并与BD延长线交于点E,求证:BD=2CE.
等腰直角三角形ABC中,∠A=90°,∠B的平分线交AC于D,过点C向BD作垂线,并与BD延长线交于点E,求证:BD=2CE.
分析 根据已知条件,易证△BFE≌△BCE,所以BF=BC,所以∠F=∠BCE,根据等腰三角形三线合一这一性质可得:CE=FE,再证明△ABD≌△ACF,证得BD=CF,从而证得BD=2CE.
解答 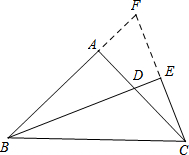 证明:延长CE,交BA延长线于点F.
证明:延长CE,交BA延长线于点F.
∵BE平分∠ABC,
∴∠ABD=∠DBC,
又∵BE⊥EC,
∴∠BEC=∠BEF=90°,
在△BEF和△BEC中,
$\left\{{\begin{array}{l}{∠ABD=∠DBC}\\{BE=BE}\\{∠BEF=∠BEC}\end{array}}\right.$,
∴△BEF≌△BEC,
∴EF=EC,
即CF=2EC,
∵AB=AC,∠BAC=90°
∴∠CAF=90°
Rt△ABD中,∠ABD+∠ADB=90°,
Rt△AEF中,∠ABD+∠F=90°,
∴∠ADB=∠F,
在△ABD和△ACF中,
$\left\{{\begin{array}{l}{∠ADB=∠F}\\{∠BAC=∠FAC}\\{AB=AC}\end{array}}\right.$,
∴△ABD≌△ACF,
∴BD=CF,
∵CF=2EC,
∴BD=2CE.
点评 本题考查了全等三角形的判定和性质,等腰三角形的性质,解题的关键是熟练应用等边对等角以及等腰三角形三线合一的性质.

练习册系列答案
相关题目
7.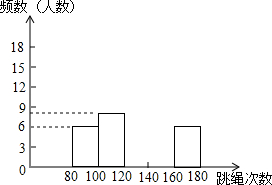 为进一步了解七年级学生的身体素质请况,老师对七年级(2)班50名学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图.如图所示:
为进一步了解七年级学生的身体素质请况,老师对七年级(2)班50名学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图.如图所示:
请结合图表完成下列问题:
(1)求表中的a;
(2)请把频数分布直方图补充完整;
(3)若七年级学生一分钟跳绳次数(x)达标要求是:80≤x<120不合格;120≤x<140为合格;140≤x<160为良;x≥160为优.为使合格率达到90%,至少还要将几人跳绳水平从不合格提高到合格或合格以上?
 为进一步了解七年级学生的身体素质请况,老师对七年级(2)班50名学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图.如图所示:
为进一步了解七年级学生的身体素质请况,老师对七年级(2)班50名学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图.如图所示:| 组 别 | 次 数x | 频数(人数) |
| 第一组 | 80≤x<100 | 6 |
| 第二组 | 100≤x<120 | 8 |
| 第三组 | 120≤x<140 | a |
| 第四组 | 140≤x<160 | 18 |
| 第五组 | 160≤x<180 | 6 |
(1)求表中的a;
(2)请把频数分布直方图补充完整;
(3)若七年级学生一分钟跳绳次数(x)达标要求是:80≤x<120不合格;120≤x<140为合格;140≤x<160为良;x≥160为优.为使合格率达到90%,至少还要将几人跳绳水平从不合格提高到合格或合格以上?
14.如图,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断地移动,每移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…那么点A2015的坐标为( )
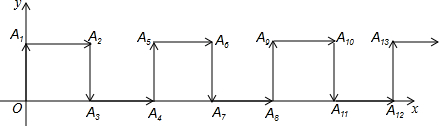

| A. | (1006,0) | B. | (1006,1) | C. | (1007,0) | D. | (1007,1) |
11. 如图,直线AB和CD相交于点O,∠AOD+∠BOC=204°,那么∠1的度数为( )
如图,直线AB和CD相交于点O,∠AOD+∠BOC=204°,那么∠1的度数为( )
 如图,直线AB和CD相交于点O,∠AOD+∠BOC=204°,那么∠1的度数为( )
如图,直线AB和CD相交于点O,∠AOD+∠BOC=204°,那么∠1的度数为( )| A. | 88° | B. | 100° | C. | 78° | D. | 109° |
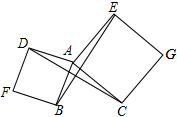 如图,以△ABC的两边AB、AC分别向外作正方形ABFD、ACGE,连接BE、DC,试猜测线段BE、DC的位置关系和数量关系,并说明理由.
如图,以△ABC的两边AB、AC分别向外作正方形ABFD、ACGE,连接BE、DC,试猜测线段BE、DC的位置关系和数量关系,并说明理由.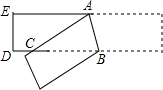 如图,将一张宽为2cm的长方形纸条折叠,折痕为AB,重叠部分为△ABC.如果∠ACB=30°,那么△ABC的面积等于4cm2.
如图,将一张宽为2cm的长方形纸条折叠,折痕为AB,重叠部分为△ABC.如果∠ACB=30°,那么△ABC的面积等于4cm2.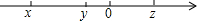 已知实数x、y、z在数轴上的对应点如图所示,化简:$\sqrt{(x-y)^{2}}$-($\sqrt{y-z}$)2+$\root{3}{(x-z)^{3}}$的值.
已知实数x、y、z在数轴上的对应点如图所示,化简:$\sqrt{(x-y)^{2}}$-($\sqrt{y-z}$)2+$\root{3}{(x-z)^{3}}$的值.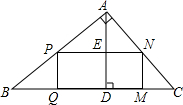 如图,△ABC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要使它加工成矩形零件PQMN,使矩形的一边在BC上,其他两个顶点分别在AB、AC上,并且PN=2PQ,PN的长是多少?
如图,△ABC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要使它加工成矩形零件PQMN,使矩形的一边在BC上,其他两个顶点分别在AB、AC上,并且PN=2PQ,PN的长是多少?