题目内容
3．
如图，大拇指与小拇指尽量张开时，两指间的距离称为指距．某项研究表明，一般情况下人的身高（ycm）是指距（xcm）的一次函数．下表是测得的一组数据：| 指距x（cm） | 19 | 20 | 21 |
| 身高y（cm） | 151 | 160 | 169 |
（2）如果李华的指距为22cm，那么他的身高的为多少？
分析 （1）设y与x的函数关系式为y=kx+b，运用待定系数法求出解析式再将数值代入解析式；
（2）将x=22代入解析式求出其y的值即可．
解答 解：（1）设y与x的函数关系式为y=kx+b，由题意，得
$\left\{\begin{array}{l}{160=20k+b}\\{169=21k+b}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{k=9}\\{b=-20}\end{array}\right.$，
∴一次函数的解析式为：y=9x-20；
（2）当x=22时，9×22-20=178，
答：他的身高的为178cm．
点评 本题考查了运用待定系数法求一次函数的解析式的运用，运用函数值求自变量的值的运用，解答时求出一次函数的解析式是关键．
练习册系列答案
相关题目
C. ﹣17 D. ﹣
B. 
C. 
D. 
11．适合下列条件的△ABC，直角三角形的个数为（ ）
①a=1，b=2，c=$\sqrt{3}$；
②∠A：∠B：∠C=3：4：5；
③a2-b2=c2；
④∠A+∠B=∠C；
⑤a=$\frac{1}{3}$，b=$\frac{1}{4}$，c=$\frac{1}{5}$．
①a=1，b=2，c=$\sqrt{3}$；
②∠A：∠B：∠C=3：4：5；
③a2-b2=c2；
④∠A+∠B=∠C；
⑤a=$\frac{1}{3}$，b=$\frac{1}{4}$，c=$\frac{1}{5}$．
| A． | 2个 | B． | 3个 | C． | 4个 | D． | 5个 |
电力公司为鼓励市民节约用电，采取按月用电量分段收费办法．若某户居民每月应交电费y（元）与用电量x（度）的函数图象是一条折线（如图所示），根据图象解下列问题：
已知一次函数图象经过点（3，2），（-1，-6）两点．
12．
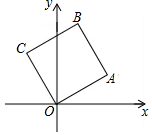如图，点A在第一象限内，其坐标为（2，1），以OA为边在x轴上方作正方形OABC，则正方形OABC的顶点C的坐标是（ ）
如图，点A在第一象限内，其坐标为（2，1），以OA为边在x轴上方作正方形OABC，则正方形OABC的顶点C的坐标是（ ）| A． | （-2，1） | B． | （1，3） | C． | （1，2） | D． | （-1.2） |
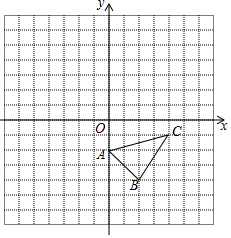已知：如图，已知△ABC．