题目内容
16. 如图,在平面直角坐标系中,点 B的坐标是(-2,0),点A是y轴正方向上的一点,且∠BAO=30°,现将△BAO顺时针旋转90°至△DCO,直线l是线段BC的垂直平分线,点P是l上一动点,则PA+PB的最小值为( )
如图,在平面直角坐标系中,点 B的坐标是(-2,0),点A是y轴正方向上的一点,且∠BAO=30°,现将△BAO顺时针旋转90°至△DCO,直线l是线段BC的垂直平分线,点P是l上一动点,则PA+PB的最小值为( )| A. | 2$\sqrt{6}$ | B. | 4 | C. | 2$\sqrt{3}$+1 | D. | 2$\sqrt{3}$+2 |
分析 根据已知条件得到OA=2$\sqrt{3}$,根据旋转的性质得到OC=OA=2$\sqrt{3}$,由直线l是线段BC的垂直平分线,得到点B,C关于直线l对称,连接AC角直线l于P,于是得到AC的长度=PA+PB的最小值,根据勾股定理即可得到结论.
解答  解:∵点 B的坐标是(-2,0),
解:∵点 B的坐标是(-2,0),
∴OB=2,
∵∠BAO=30°,
∴OA=2$\sqrt{3}$,
∵现将△BAO顺时针旋转90°至△DCO,
∴OC=OA=2$\sqrt{3}$,
∵直线l是线段BC的垂直平分线,
∴点B,C关于直线l对称,
连接AC交直线l于P,
则此时AC的长度=PA+PB的最小值,
∵AC=$\sqrt{O{A}^{2}+O{C}^{2}}$=2$\sqrt{6}$,
∴PA+PB的最小值为2$\sqrt{6}$,
故选A.
点评 本题考查的是轴对称-最短路线问题,线段垂直平分线的性质,解答此题的关键是找到点B的对称点,把题目的问题转化为两点之间线段最短解答.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
7.张师傅和李师傅两人加工同一种零件,张师傅每小时比李师傅多加工5个零件,张师傅加工120个零件与李师傅加工100个零件所用的时间相同.设张师傅每小时加工零件x个,依题意,可列方程为( )
| A. | $\frac{120}{x+5}=\frac{100}{x}$ | B. | $\frac{120}{x}=\frac{100}{x+5}$ | C. | $\frac{120}{x}=\frac{100}{x-5}$ | D. | $\frac{120}{x-5}=\frac{100}{x}$ |
11.若等腰三角形的周长为26cm,一边为11cm,则腰长为( )
| A. | 11 cm | B. | 7.5 cm | C. | 11 cm或7.5 cm | D. | 以上都不对 |
1.下列关于x的方程:①ax2+bx+c=0;②3(x-9)2-(x+1)2=1;③x+3=$\frac{1}{x}$;④x2=0;⑤$\sqrt{x+1}=x-1$.其中是一元二次方程有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
5.若点P(m-1,3)在第二象限,则m的取值范围是( )
| A. | m>1 | B. | m<1 | C. | m≥-1 | D. | m≤1 |
17.若x>y,则下列等式不一定成立的是( )
| A. | x+4>y+4 | B. | -3x<-3y | C. | $\frac{x}{3}>\frac{y}{3}$ | D. | x2>y2 |
 如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,过E点作EF∥DC交BC的延长线于点F,连接CD.
如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,过E点作EF∥DC交BC的延长线于点F,连接CD.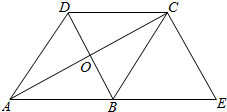 如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连结CE,若∠E=50°,求∠BAO的大小.
如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连结CE,若∠E=50°,求∠BAO的大小.