题目内容
17.解方程:(1)(x-1)2=9;
(2)x2+4x-1=0;
(3)x2+3=3(x+1);
(4)x2+3x-4=0.
分析 (1)直接开方求得方程的解;
(2)利用配方法求得方程的解;
(3)移项,化为一般形式,利用因式分解法求得方程的解;
(4)利用因式分解法求得方程的解.
解答 解:(1)(x-1)2=9
x-1=±3
x-1=3,x-1=-3
解得:x1=4,x2=-2;
(2)x2+4x-1=0
x2+4x=1
x2+4x+4=5
(x+2)2=5
x+2=±$\sqrt{5}$
解得:x1=-2+$\sqrt{5}$,x2=-2-$\sqrt{5}$;
(3)x2+3=3(x+1)
整理得x2-3x=0
x(x-3)=0
x=0,x-3=0
解得:x1=0,x2=3;
(4)x2+3x-4=0
(x+4)(x-1)=0
x+4=0,x-3=0
解得:x1=-4,x2=3.
点评 此题考查解一元二次方程,掌握解方程的步骤与方法,根据方程的特点选择合适的解法是解决问题的关键.

练习册系列答案
相关题目
9.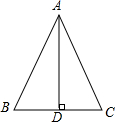 如图,AD⊥BC,且AB=AC,则判定△ABD≌△ACD的最好理由是( )
如图,AD⊥BC,且AB=AC,则判定△ABD≌△ACD的最好理由是( )
 如图,AD⊥BC,且AB=AC,则判定△ABD≌△ACD的最好理由是( )
如图,AD⊥BC,且AB=AC,则判定△ABD≌△ACD的最好理由是( )| A. | ASA | B. | SAS | C. | SSS | D. | HL |
7.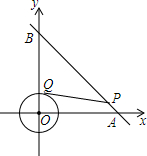 如图,⊙O是以原点为圆心,2为半径的圆,点P是直线y=-x+4上的一点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为( )
如图,⊙O是以原点为圆心,2为半径的圆,点P是直线y=-x+4上的一点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为( )
 如图,⊙O是以原点为圆心,2为半径的圆,点P是直线y=-x+4上的一点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为( )
如图,⊙O是以原点为圆心,2为半径的圆,点P是直线y=-x+4上的一点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为( )| A. | 3 | B. | 2 | C. | 3-$\sqrt{2}$ | D. | 2 $\sqrt{2}$ |
 如图,△ABC中,AB=AC=10cm,BD⊥AC于点D,且BD=6cm,动点P从点B出发,以1cm/s的速度,沿B→A的方向运动,到达点A时停止,动点Q从点A出发,以2cm/s的速度,沿A→C的方向运动,到达点C时停止,P、Q两点同时出发,设运动的时间为t(s),△APQ的面积为S(cm2),则S关于t的函数图象大致为( )
如图,△ABC中,AB=AC=10cm,BD⊥AC于点D,且BD=6cm,动点P从点B出发,以1cm/s的速度,沿B→A的方向运动,到达点A时停止,动点Q从点A出发,以2cm/s的速度,沿A→C的方向运动,到达点C时停止,P、Q两点同时出发,设运动的时间为t(s),△APQ的面积为S(cm2),则S关于t的函数图象大致为( )



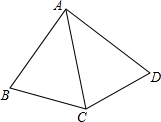 如图,在四边形ABCD中,AC平分∠BAD,AC2=AB•AD.试说明∠BCD=∠B+∠D的理由.
如图,在四边形ABCD中,AC平分∠BAD,AC2=AB•AD.试说明∠BCD=∠B+∠D的理由. 如图,点A(t,4)在第一象限,OA与x轴所夹的锐角为α,tanα=$\frac{4}{3}$,则t的值为3.
如图,点A(t,4)在第一象限,OA与x轴所夹的锐角为α,tanα=$\frac{4}{3}$,则t的值为3.