题目内容
11.已知二次函数y=-x2+10x-17,若y的值小于等于8,且大于等于4,则x的取值范围是3≤x≤7.分析 先利用配方法求得y的最大值为8,然后令y=4求得x的值,然后根据二次函数的性质可求得x的取值范围.
解答 解:y=-x2+10x-17
=-(x2-10x+25-25)-17
=-(x-5)2+25-17
=-(x-5)2+8.
∴y的最大值为8.
令y=4得:-x2+10x-17=4,解得:x1=3,x2=7.
∴3≤x≤7.
故答案为:3≤x≤7.
点评 本题主要考查的是二次函数的性质,掌握二次函数的性质是解题的关键.

练习册系列答案
相关题目
19.甲、乙两名同学本学期参加的11次考试成绩(单位:分)如下表所示:
(1)求两人的平均分及方差;
(2)分析他们的成绩各有什么特点;
(3)现要从两人中选一人参加比赛,历届比赛成绩表明,平均成绩达98分以上(含98分)才可能迸人决赛,你认为应该选谁参加这次比赛呢?为什么?
| 甲 | 98 | 100 | 100 | 90 | 96 | 91 | 89 | 99 | 100 | 100 | 93 |
| 乙 | 98 | 99 | 96 | 94 | 95 | 92 | 92 | 98 | 96 | 99 | 97 |
(2)分析他们的成绩各有什么特点;
(3)现要从两人中选一人参加比赛,历届比赛成绩表明,平均成绩达98分以上(含98分)才可能迸人决赛,你认为应该选谁参加这次比赛呢?为什么?
3.解关于x的方程4x-ax=5时,合并同类项得5x=5,则a的值为( )
| A. | 0 | B. | 1 | C. | 5 | D. | -1 |
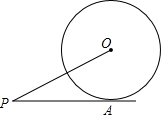 如图,已知PA切⊙O于点A,OP=5,PA比⊙O的半径大1,求⊙O的半径.
如图,已知PA切⊙O于点A,OP=5,PA比⊙O的半径大1,求⊙O的半径.