题目内容
11.某汽车专卖店销售A,B两种型号的新能源汽车.上周售出1辆A型车和3辆B型车,销售额为96万元;本周已售出2辆A型车和1辆B型车,销售额为62万元.(1)求每辆A型车和B型车的售价各为多少元.
(2)甲公司拟向该店购买A,B两种型号的新能源汽车共6辆,购车费不少于130万元,且不超过140万元.则有哪几种购车方案?
分析 (1)每辆A型车和B型车的售价分别是x万元、y万元.则等量关系为:1辆A型车和3辆B型车,销售额为96万元,2辆A型车和1辆B型车,销售额为62万元;
(2)设购买A型车a辆,则购买B型车(6-a)辆,则根据“购买A,B两种型号的新能源汽车共6辆,购车费不少于130万元,且不超过140万元”得到不等式组.
解答 解:(1)每辆A型车和B型车的售价分别是x万元、y万元.则
$\left\{\begin{array}{l}{x+3y=96}\\{2x+y=62}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=18}\\{y=26}\end{array}\right.$.
答:每辆A型车的售价为18万元,每辆B型车的售价为26万元;
(2)设购买A型车a辆,则购买B型车(6-a)辆,则依题意得
$\left\{\begin{array}{l}{18a+26(6-a)≥130}\\{18a+26(6-a)≤140}\end{array}\right.$,
解得 2≤a≤3$\frac{1}{4}$.
∵a是正整数,
∴a=2或a=3.
∴共有两种方案:
方案一:购买2辆A型车和4辆B型车;
方案二:购买3辆A型车和3辆B型车.
点评 本题考查了一元一次不等式组的应用和二元一次方程组的应用.解决问题的关键是读懂题意,找到关键描述语,进而找到所求的量的等量关系.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案
相关题目
2.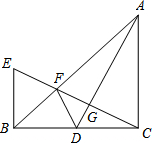 如图,在△ABC中,∠BCA=90°,CA=CB,AD为BC边上的中线,CG⊥AD于G,交AB于F,过点B作BC的垂线交CG于E.现有下列结论:①△ADC≌△CEB;②DF=CD;③∠ADC=∠BDF;④F为EG中点.其中结论正确的为( )
如图,在△ABC中,∠BCA=90°,CA=CB,AD为BC边上的中线,CG⊥AD于G,交AB于F,过点B作BC的垂线交CG于E.现有下列结论:①△ADC≌△CEB;②DF=CD;③∠ADC=∠BDF;④F为EG中点.其中结论正确的为( )
 如图,在△ABC中,∠BCA=90°,CA=CB,AD为BC边上的中线,CG⊥AD于G,交AB于F,过点B作BC的垂线交CG于E.现有下列结论:①△ADC≌△CEB;②DF=CD;③∠ADC=∠BDF;④F为EG中点.其中结论正确的为( )
如图,在△ABC中,∠BCA=90°,CA=CB,AD为BC边上的中线,CG⊥AD于G,交AB于F,过点B作BC的垂线交CG于E.现有下列结论:①△ADC≌△CEB;②DF=CD;③∠ADC=∠BDF;④F为EG中点.其中结论正确的为( )| A. | ①② | B. | ①②③ | C. | ①③ | D. | ①③④ |
3.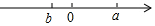 有理数a,b在数轴上的位置如图所示,则下列结论正确的是( )
有理数a,b在数轴上的位置如图所示,则下列结论正确的是( )
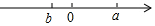 有理数a,b在数轴上的位置如图所示,则下列结论正确的是( )
有理数a,b在数轴上的位置如图所示,则下列结论正确的是( )| A. | a-b<b<a<a+b | B. | a-b<b<a+b<a | C. | b<a+b<a<a-b | D. | a+b<b<a<a-b |
 如图,小明同学沿着格线从A点到B点,在路线最短的条件下,经过C点的概率是$\frac{2}{3}$.
如图,小明同学沿着格线从A点到B点,在路线最短的条件下,经过C点的概率是$\frac{2}{3}$.