题目内容
19.已知-1<x<3,化简:|x+1|+$\sqrt{{{({x-3})}^2}}$=4.分析 首先由$\sqrt{{{({x-3})}^2}}$=|x-3|,即可将原式化简,然后由-1<x<3,去绝对值符号,继而求得答案.
解答 解:∵-1<x<3,
∴|x+1|+$\sqrt{{{({x-3})}^2}}$=|x+1|+|x-3|
=x+1+3-x
=4.
故答案为:4.
点评 此题考查了二次根式的性质与化简以及绝对值的性质.此题难度适中,注意确定各项的符号是解此题的关键.

练习册系列答案
相关题目
7.下列各式:-(-3);-|-3|;-32;(-3)4;-$\root{3}{-8}$计算结果为负数的有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
4.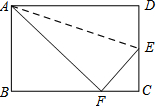 如图,折叠矩形纸片ABCD的一边AD,使点D落在BC边的点F处,已知AB=8 cm,BC=10 cm,则EC的长( )
如图,折叠矩形纸片ABCD的一边AD,使点D落在BC边的点F处,已知AB=8 cm,BC=10 cm,则EC的长( )
 如图,折叠矩形纸片ABCD的一边AD,使点D落在BC边的点F处,已知AB=8 cm,BC=10 cm,则EC的长( )
如图,折叠矩形纸片ABCD的一边AD,使点D落在BC边的点F处,已知AB=8 cm,BC=10 cm,则EC的长( )| A. | 3 cm | B. | 4 cm | C. | 5 cm | D. | 6 cm |
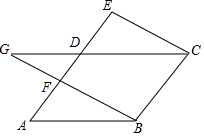 如图,在?ABCD中,AD=4,AB=5,延长AD到点E,连接EC过点B作BF∥CE交AD于点F,交CD的延长线于点G.
如图,在?ABCD中,AD=4,AB=5,延长AD到点E,连接EC过点B作BF∥CE交AD于点F,交CD的延长线于点G.