��Ŀ����
17��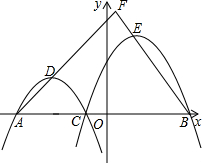 ��ͼ����ƽ��ֱ������ϵxOy�У���֪A��B���������ֱ�Ϊ��-4��0������4��0����C��m��0�����߶�A B��һ�㣨�� A��B�㲻�غϣ���������L1��y=ax2+b1x+c1��a��0��������A��C������ΪD��������L2��y=ax2+b2x+c2��a��0��������C��B������ΪE��AD��BE���ӳ����ཻ�ڵ�F��
��ͼ����ƽ��ֱ������ϵxOy�У���֪A��B���������ֱ�Ϊ��-4��0������4��0����C��m��0�����߶�A B��һ�㣨�� A��B�㲻�غϣ���������L1��y=ax2+b1x+c1��a��0��������A��C������ΪD��������L2��y=ax2+b2x+c2��a��0��������C��B������ΪE��AD��BE���ӳ����ཻ�ڵ�F����1����a=-$\frac{1}{2}$��m=-1����������L1��L2�Ľ���ʽ��
��2����a=-1��AF��BF����m��ֵ��
��3���Ƿ����������ʵ��a��a��0��������mȡ��ֵ��ֱ��AF��BF�������ܻ��ഹֱ�������ڣ���ֱ��д��a��������ͬ��ֵ���������ڣ���˵�����ɣ�
���� ��1�����ô���ϵ��������A��B��C������������ʽ������ö��κ����Ľ���ʽ��
��2������D��DG��x���ڵ�G������E��EH��x���ڵ�H����֤��ADG����EBH���������������ζ�Ӧ�߱�����ȼ��ɽ��⣻
��3�������Դ𰸣����뷨���ɽ��⣻
��� �⣺��1����A��C�����y=ax2+b1x+c1�У��ɵã�$\left\{\begin{array}{l}{-\frac{1}{2}{����-1��}^{2}{-b}_{1}{+c}_{1}=0}\\{-\frac{1}{2}{����-4��}^{2}-{4b}_{1}{+c}_{1}=0}\end{array}\right.$����ã�$\left\{\begin{array}{l}{{b}_{1}=-\frac{5}{2}}\\{{c}_{1}=-2}\end{array}\right.$��
��������L1����ʽΪy=$-\frac{1}{2}{x}^{2}-\frac{5}{2}x-2$��
ͬ���ɵã�$\left\{\begin{array}{l}{-\frac{1}{2}{����-1��}^{2}{-b}_{2}{+c}_{2}=0}\\{-\frac{1}{2}{��4}^{2}+{4b}_{2}{+c}_{2}=0}\end{array}\right.$����ã�$\left\{\begin{array}{l}{{b}_{2}=\frac{3}{2}}\\{{c}_{2}=2}\end{array}\right.$��
��������L2����ʽΪy=$-\frac{1}{2}{x}^{2}-\frac{5}{2}x-2$��
��2����ͼ������D��DG��x���ڵ�G������E��EH��x���ڵ�H��
������ã�$\left\{\begin{array}{l}{0=-16-{4b}_{1}{+c}_{1}}\\{0{=-m}^{2}{+b}_{1}m{+c}_{1}}\end{array}\right.$����ã�$\left\{\begin{array}{l}{{b}_{1}=m-4}\\{{c}_{1}=4m}\end{array}\right.$��
��������L1����ʽΪy=-x2+��m-4��x+4m��
���D������$\frac{m-4}{2}$��$\frac{{m}^{2}+8m+16}{4}$����
��DG=$\frac{{m}^{2}+8m+16}{4}$=$\frac{{��m+4��}^{2}}{4}$��AG=$\frac{m+4}{2}$��
ͬ���ɵã�������L2����ʽΪy=-x2+��m+4��x-4m��
��EH=$\frac{{m}^{2}-8m+16}{4}$=$\frac{{��m-4��}^{2}}{4}$��BH=$\frac{4-m}{2}$��
��AF��BF��DG��x�ᣬEH��x�ᣬ
���AFB=��AGD=��EHB=90�㣬
�ߡ�DAG+��ADG=90�㣬��DAG+��EBH=90�㣬
���ADG=��EBH��
���ڡ�ADG�͡�EBH�У�
$\left\{\begin{array}{l}{��ADG=��EBH}\\{��AGD=��EHB=90��}\end{array}\right.$��
���ADG����EBH��
��$\frac{DG}{BH}$=$\frac{AG}{EH}$��
��$\frac{\frac{{��m+4��}^{2}}{4}}{\frac{4-m}{2}}$=$\frac{\frac{m+4}{2}}{\frac{{��m-4��}^{2}}{4}}$������ã�m2=12��
��ã�m=��$2\sqrt{3}$��
��3�����ڣ����磺a=-$\frac{1}{3}$��-$\frac{1}{4}$��
��a=-$\frac{1}{3}$ʱ������A��C������ã�
������L1����ʽΪy=-$\frac{1}{3}$x2+$\frac{1}{3}$��m-4��x+$\frac{4}{3}$m��
ͬ���ɵã�������L2����ʽΪy=-$\frac{1}{3}$x2+$\frac{1}{3}$��m+4��x-$\frac{4}{3}$m��
���D������$\frac{m-4}{2}$��$\frac{{��m+4��}^{2}}{12}$������E������$\frac{m+4}{2}$��$\frac{{��m-4��}^{2}}{12}$����
��ֱ��AFб��Ϊ$\frac{\frac{{��m+4��}^{2}}{12}}{\frac{4+m}{2}}$��ֱ��BFб��Ϊ$\frac{\frac{{��m-4��}^{2}}{12}}{\frac{m-4}{2}}$��
��ҪAF��BF����ֱ��AF��BFб�ʳ˻�Ϊ-1��
��$\frac{\frac{{��m+4��}^{2}}{12}}{\frac{4+m}{2}}$��$\frac{\frac{{��m-4��}^{2}}{12}}{\frac{m-4}{2}}$=-1������ã�m2=-20���⣻
ͬ�������a=-$\frac{1}{4}$���⣮
���� ���⿼���˴���ϵ���������ʽ�������������������ε��ж������������ζ�Ӧ�߱�����ȵ����ʣ��������������߲�֤����ADG����EBH�ǽ���Ĺؼ���

| A�� | 30�� | B�� | 60���120�� | C�� | 150�� | D�� | 30���150�� |
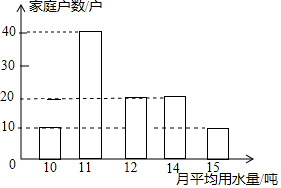 Ϊ�˳�������Լ��ˮ���������𡱣���������������ֱ����500����ͥ����ˮ�����һ�ε��飬����������С��������������100����ͥһ�����ƽ����ˮ������λ���֣����������������Ƴ�����ͼ��ʾ������ͳ��ͼ�����������ݵ���������λ���ֱ��ǣ�������
Ϊ�˳�������Լ��ˮ���������𡱣���������������ֱ����500����ͥ����ˮ�����һ�ε��飬����������С��������������100����ͥһ�����ƽ����ˮ������λ���֣����������������Ƴ�����ͼ��ʾ������ͳ��ͼ�����������ݵ���������λ���ֱ��ǣ�������| A�� | 40��20 | B�� | 11��11 | C�� | 11��12 | D�� | 11��11.5 |
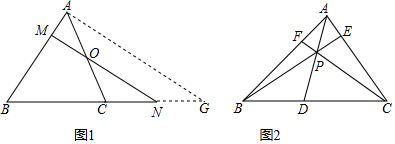
 ��ͼ����֪��ABC�ڽ��ڡ�O����C���ӻ�AB�ϣ������A��B�غϣ�����DΪ��BC���е㣬DE��BC��DE��AC���ӳ��߽��ڵ�E������AO������EB���ڵ�F�����O���ڵ�G�����GAB=������ACB=�£���EAG+��EBA=�ã�
��ͼ����֪��ABC�ڽ��ڡ�O����C���ӻ�AB�ϣ������A��B�غϣ�����DΪ��BC���е㣬DE��BC��DE��AC���ӳ��߽��ڵ�E������AO������EB���ڵ�F�����O���ڵ�G�����GAB=������ACB=�£���EAG+��EBA=�ã���1�����ͬѧͨ����ͼ�Ͳ����õ����½������ݣ�
| �� | 30�� | 40�� | 50�� | 60�� |
| �� | 120�� | 130�� | 140�� | 150�� |
| �� | 150�� | 140�� | 130�� | 120�� |
��2������=135�㣬CD=3����ABE�����Ϊ��ABC�������4�������O�뾶�ij���
| A�� | 20% | B�� | 25% | C�� | 50% | D�� | 62.5% |