题目内容
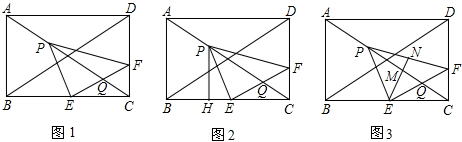
1.已知:如图1,矩形ABCD中,AB=6cm,BC=8cm,点E从点C出发,沿CB方向匀速向点B运动,速度为每秒4cm,同时点P从点A出发,沿AC方向匀速向向点C运动,速度为每秒5cm,过点E平行于BD的直线EF,交CD于F,交AC于Q,当点P运动到线段EF上时,点P、点E都停止运动.设运动时间为t秒,△PEF的面积为y(cm2)(1)当t=$\frac{4}{3}$时,点P恰好运动到线段EF上;(请直接写出答案)
(2)如图2,过点P作PH⊥BC于H,当t为何值时,△PEH∽△EFC?
(3)求y关于t的函数关系式;
(4)如图3,取PF的中点N,连接EN,交AC于M,请问随着时间t的改变,点M的位置会发生改变吗?如果会改变请说明点M的变化情况;如果不会改变,请求出点M的具体位置.
分析 (1)当点P运动到线段EF上时,则CE=4t,AP=5t,再由EF∥BD得出△CPE∽△CGB,由相似三角形的性质得出PC的长,进而可得出结论;
(2)过点P作PG⊥AB于点G,根据BC⊥AB可知△AGP∽△ABC,故可得出AG,GP的长,再根据△PEH∽△EFC即可得出t的值;
(3)根据S△PEF=S梯形PHCF-S△EFC-S△PHE即可得出结论;
(4)只要证明PQ、EN是△PEF的中线,得到MQ=$\frac{1}{3}$PQ=$\frac{10}{3}$-$\frac{5}{2}$t,求出CM即可解决问题.
解答 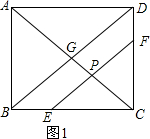 解:(1)如图1,当点P运动到线段EF上时,则CE=4t,AP=5t,
解:(1)如图1,当点P运动到线段EF上时,则CE=4t,AP=5t,
∵矩形ABCD中,AB=6cm,BC=8cm,
∴AC=BD=$\sqrt{{6}^{2}+{8}^{2}}$=10cm.
∵EF∥BD,
∴△CPE∽△CGB,
∴$\frac{PC}{CG}$=$\frac{CE}{BC}$,即$\frac{PC}{5}$=$\frac{4t}{8}$,解得PC=2.5t,∵AC=QP+PC=5t+2.5t=10,
∴t=$\frac{4}{3}$.
故答案为:$\frac{4}{3}$;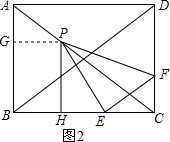
(2)如图2,过点P作PG⊥AB于点G,
∵BC⊥AB,
∴PG∥BC,
∴△AGP∽△ABC,
∵△PEH∽△EFC,
∴$\frac{PH}{EC}$=$\frac{EH}{FC}$,
∴$\frac{6-3t}{4t}$=$\frac{8-8t}{3t}$
解得t=$\frac{14}{23}$(秒);
(3)S△PEF=S梯形PHCF-S△EFC-S△PHE
=$\frac{1}{2}$(PH+FC)•HC-$\frac{1}{2}$PH•HE-$\frac{1}{2}$EC•FC
=3(8-4t)-$\frac{1}{2}$(6-3t)(8-8t)-2t•3t
=24-12t-12t2+36t-24-6t2
=-18t2+24t,即y=-18t2+24t;
(4)不变.
如图3,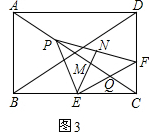 由题意可知:PA=5t.CE=4t,AO=CO=BO=OD=5,
由题意可知:PA=5t.CE=4t,AO=CO=BO=OD=5,
∵EF∥BD,
∴$\frac{CQ}{CO}$=$\frac{CE}{CB}$,$\frac{EQ}{BO}$=$\frac{QF}{OD}$=$\frac{CQ}{CO}$,
∴$\frac{CQ}{5}$=$\frac{4t}{8}$,EQ=QF
∴CQ=$\frac{5}{2}$t,PQ=10-5t-$\frac{5}{2}$t=10-$\frac{15}{2}$t
∵PQ、EN是△PEF的中线,
∴MQ=$\frac{1}{3}$PQ=$\frac{10}{3}$-$\frac{5}{2}$t.,
∴CM=MQ+CQ=$\frac{10}{3}$,
∴点M是定点.
点评 本题考查的是四边形综合题,涉及到矩形的性质、相似三角形的判定与性质、用待定系数法求一次函数的解析式等知识,难度较大.

 灵星计算小达人系列答案
灵星计算小达人系列答案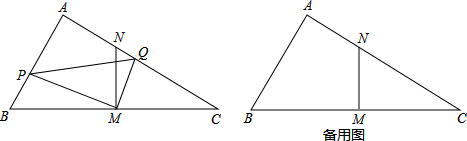
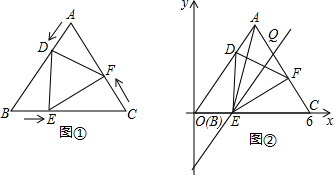
 某赛季甲、乙两名篮球运动员12场比赛得分情况用图表示如下:
某赛季甲、乙两名篮球运动员12场比赛得分情况用图表示如下: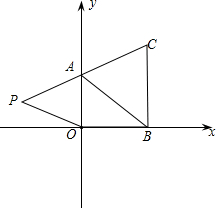 如图,在下面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a、b、c满足关系式|a-2|+(b-3)2=0和(c-4)2≤0;
如图,在下面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a、b、c满足关系式|a-2|+(b-3)2=0和(c-4)2≤0;