题目内容
16.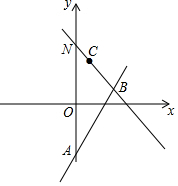 如图,平面直角坐标系中,直线y=2x+m与y轴交于点A,点直线y=-x+5交于点B(4,n),C为直线y=-x+5上任意一点
如图,平面直角坐标系中,直线y=2x+m与y轴交于点A,点直线y=-x+5交于点B(4,n),C为直线y=-x+5上任意一点(1)求m,n的值,;
(2)求使线段AC长度最短时点C的坐标,并得出AC的最小值为6$\sqrt{2}$.
分析 (1)首先把点B(4,n)代入直线y=-x+5得出n的值,再把B点坐标代入直线y=2x+m求得m的值即可;
(2)过点A作直线y=-x+5的垂线,垂足为C,作CM⊥AN于M.利用等腰直角三角形的性质和勾股定理解决问题.
解答 解:(1)∵点B(4,n)在直线上y=-x+5,
∴n=-4+5=1,B(4,1).
∵点B(4,1)在直线上y=2x+m上,
∴8+m=1,解得m=-7; (2)过点A作直线y=-x+5的垂线,垂足为C,此时线段AC最短.作CM⊥AN于M.
(2)过点A作直线y=-x+5的垂线,垂足为C,此时线段AC最短.作CM⊥AN于M.
∵直线y=-x+5与y轴交点N(0,5),直线y=2x-7与y轴交点A(0,-7),
∴AN=12,∠ANC=45°,
∵∠ACN=90°,
∴AC=CN,
∵CM⊥AN,
∴AM=CM=6,AC=6$\sqrt{2}$,
∴OM=1,
∴C(6,-1).
故答案为6$\sqrt{2}$.
点评 本题考查了一次函数图象上点的坐标特征与垂线段最短的性质,结合图形,选择适当的方法解决问题.

练习册系列答案
相关题目
7.下列各数中,最小的数是( )
| A. | 0 | B. | $\frac{π}{3}$ | C. | -$\sqrt{5}$ | D. | -3 |
4.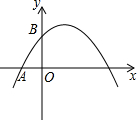 如图,抛物线y=-x2+ax+4与x轴负半轴交于点A,与y轴交于点B,且tan∠ABO=$\frac{1}{4}$,点C(x1,y1),D(x2,y2)是抛物线y=-x2+ax+4上两点,当x1≤x≤x2,y的取值范围为$\frac{12}{{x}_{2}}$≤y≤$\frac{12}{{x}_{1}}$.则下列结论正确的是( )
如图,抛物线y=-x2+ax+4与x轴负半轴交于点A,与y轴交于点B,且tan∠ABO=$\frac{1}{4}$,点C(x1,y1),D(x2,y2)是抛物线y=-x2+ax+4上两点,当x1≤x≤x2,y的取值范围为$\frac{12}{{x}_{2}}$≤y≤$\frac{12}{{x}_{1}}$.则下列结论正确的是( )
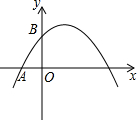 如图,抛物线y=-x2+ax+4与x轴负半轴交于点A,与y轴交于点B,且tan∠ABO=$\frac{1}{4}$,点C(x1,y1),D(x2,y2)是抛物线y=-x2+ax+4上两点,当x1≤x≤x2,y的取值范围为$\frac{12}{{x}_{2}}$≤y≤$\frac{12}{{x}_{1}}$.则下列结论正确的是( )
如图,抛物线y=-x2+ax+4与x轴负半轴交于点A,与y轴交于点B,且tan∠ABO=$\frac{1}{4}$,点C(x1,y1),D(x2,y2)是抛物线y=-x2+ax+4上两点,当x1≤x≤x2,y的取值范围为$\frac{12}{{x}_{2}}$≤y≤$\frac{12}{{x}_{1}}$.则下列结论正确的是( )| A. | a=-3 | B. | y2<4 | C. | |x1-x2|=1 | D. | |x1-$\frac{3}{2}$|>|x2-$\frac{3}{2}$| |
11.九一(1)班在参加学校4×100m接力赛时,安排了甲,乙,丙,丁四位选手,他们的顺序由抽签随机决定,则甲跑第一棒的概率为( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
8.下列图形中,∠2>∠1的是( )
| A. |  | B. |  平行四边形 | C. |  | D. |  |
6.同时抛掷两枚质地均匀的硬币,两枚硬币全部正面向上的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |


 如图,⊙M的圆心M(-1,2),⊙M经过坐标原点O,与y轴交于点A.经过点A的一条直线l解析式为:y=-$\frac{1}{2}$x+4与x轴交于点B,以M为顶点的抛物线经过x轴上点D(2,0)和点C(-4,0).
如图,⊙M的圆心M(-1,2),⊙M经过坐标原点O,与y轴交于点A.经过点A的一条直线l解析式为:y=-$\frac{1}{2}$x+4与x轴交于点B,以M为顶点的抛物线经过x轴上点D(2,0)和点C(-4,0).