题目内容
15.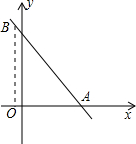 如图所示,平面直角坐标系中有一直线AB与x轴夹角为60°,且点A坐标为(3,0),点B在x轴上方,设AB=k,那么点B的横坐标为( )
如图所示,平面直角坐标系中有一直线AB与x轴夹角为60°,且点A坐标为(3,0),点B在x轴上方,设AB=k,那么点B的横坐标为( )| A. | 3-$\frac{k}{2}$ | B. | 3+$\frac{k}{2}$ | C. | $\frac{k}{2}$ | D. | -$\frac{k}{2}$-3 |
分析 先根据三角函数求出AD的值,由此即可得出B点的横坐标.
解答  解;作BD⊥x轴于D,
解;作BD⊥x轴于D,
∵∠OAB=60°,AB=k,
∴在RT△ABD中,cos∠OAB=$\frac{AD}{AB}$,
即cos60°=$\frac{AD}{k}$,
∴OD=$\frac{k}{2}$,
∵A坐标为(3,0),
∴OA=3,
∴OD=OD-OA=$\frac{k}{2}$-3,
∴D的坐标为(3-$\frac{k}{2}$,0),
∴点B的横坐标为3-$\frac{k}{2}$.
故选A.
点评 本题主要考查了一次函数图象上点的坐标特征以及三角函数的应用,熟练掌握直角三角函数是解题的关键.

练习册系列答案
相关题目
5.某反比例函数的图象经过点(-1,3),则此函数的图象也经过点( )
| A. | (-1,-3) | B. | (-3,1) | C. | (1,3) | D. | (-3,-1) |
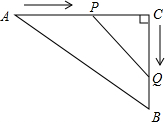 如图,在△ABC中,AC=50m,BC=40m,点A开始沿AC边向点C以2m/s的速度匀速移动,同时另一点Q由C点开始以3m/s的速度沿着CB匀速移动,几秒后,△PCQ与△ABC相似?
如图,在△ABC中,AC=50m,BC=40m,点A开始沿AC边向点C以2m/s的速度匀速移动,同时另一点Q由C点开始以3m/s的速度沿着CB匀速移动,几秒后,△PCQ与△ABC相似?
 如图,已知△ABC.
如图,已知△ABC.