题目内容
2.观察图形: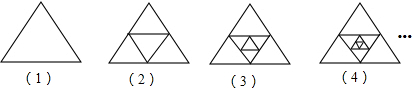
把图形中间的三角形的各边中点顺次相连,得到后一图形.第1个图中有1个三角形,第2个图中有5个三角形,第3个图中有9个三角形,….按此规律,第n个图中有(4n-3)个三角形.(用正整数n表示)
分析 图1三角形的个数为4×1-3=1,图2三角形的个数为4×2-3=5,图3三角形的个数为4×3-3=9,可以发现:第几个图形中三角形的个数就是4与几的乘积减去3,按照这个规律即可求出第n各图形中有多少三角形.
解答 解:分别数出图1、图2、图3中的三角形的个数,
图1中三角形的个数为4×1-3=1;
图2中三角形的个数为4×2-3=5;
图3中三角形的个数为4×3-3=9;
…
可以发现,第几个图形中三角形的个数就是4与几的乘积减去3.
按照这个规律,如果设图形的个数为n,那么其中三角形的个数为4n-3.
故答案为:4n-3.
点评 此题主要考查学生对图形变化类这个知识点的理解和掌握,解答此类题目的关键是根据题目中给出的图形,通过观察思考,归纳总结出规律,此类题目难度一般偏大,属于难题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
12. 张浩调查统计了他们家5月份每次打电话的通话时长,并将统计结果进行分组(每组含量最小值,不含最大值),将分组后的结果绘制成如图所示的频数分布直方图,则下列说法中不正确的是( )
张浩调查统计了他们家5月份每次打电话的通话时长,并将统计结果进行分组(每组含量最小值,不含最大值),将分组后的结果绘制成如图所示的频数分布直方图,则下列说法中不正确的是( )
 张浩调查统计了他们家5月份每次打电话的通话时长,并将统计结果进行分组(每组含量最小值,不含最大值),将分组后的结果绘制成如图所示的频数分布直方图,则下列说法中不正确的是( )
张浩调查统计了他们家5月份每次打电话的通话时长,并将统计结果进行分组(每组含量最小值,不含最大值),将分组后的结果绘制成如图所示的频数分布直方图,则下列说法中不正确的是( )| A. | 张浩家5月份打电话的总频数为80次 | |
| B. | 张浩家5月份每次打电话的通话时长在5-10分钟的频数为15次 | |
| C. | 张浩家5月份每次打电话的通话时长在10-15分钟的频数最多 | |
| D. | 张浩家5月份每次打电话的通话时长在20-25分钟的频率为6% |
13.如果盈利20元记作+20,那么亏本50元记作( )
| A. | +50元 | B. | -50元 | C. | +20元 | D. | -20元 |
10.八年级学生去距学校11km的科技馆参观,一部分学生骑自行车,过了20min后,其余学生乘汽车出发,结果他们同时到达.已知汽车的速度是骑车学生速度的2倍,求骑车学生的速度,设骑车学生的速度为xkm/h,则所列方程正确的是( )
| A. | $\frac{11}{x}=\frac{11}{2x}-\frac{1}{3}$ | B. | $\frac{11}{x}=\frac{11}{2x}-20$ | C. | $\frac{11}{x}=\frac{11}{2x}+\frac{1}{3}$ | D. | $\frac{11}{x}=\frac{11}{2x}+20$ |
11. 如图,正三角形ABC是⊙O的内接三角形,点P是劣弧AB上不同于点A、B的任意一点,则∠BPC的度数是( )
如图,正三角形ABC是⊙O的内接三角形,点P是劣弧AB上不同于点A、B的任意一点,则∠BPC的度数是( )
 如图,正三角形ABC是⊙O的内接三角形,点P是劣弧AB上不同于点A、B的任意一点,则∠BPC的度数是( )
如图,正三角形ABC是⊙O的内接三角形,点P是劣弧AB上不同于点A、B的任意一点,则∠BPC的度数是( )| A. | 30° | B. | 45° | C. | 50° | D. | 60° |