题目内容
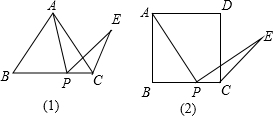 (1)在正△ABC中,P在BC上,∠APE=∠B,PE与∠C的外角平分线交于E,求证:AP=PE.
(1)在正△ABC中,P在BC上,∠APE=∠B,PE与∠C的外角平分线交于E,求证:AP=PE.(2)如图(2),(1)中“在正△ABC 中“改为“在正方形ABCD中“,其余不变,其结论仍然成立吗?
考点:全等三角形的判定与性质,等边三角形的性质,正方形的性质
专题:
分析:(1)连接AE,可证点A、C、P、E四点共圆,进而可以证明∠PAE=60°,即可证明△APE是等边三角形,即可解题;
(2)连接AE,取AG=CP,连接GP,易证∠EPC=∠PAB,∠AGP=∠ECP,即可证明△AGP和△PCE,即可解题.
(2)连接AE,取AG=CP,连接GP,易证∠EPC=∠PAB,∠AGP=∠ECP,即可证明△AGP和△PCE,即可解题.
解答:解:(1)连接AE,
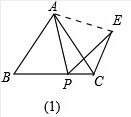
∵CE是等边△ABC的外角平分线,
∴∠ACE=∠DCE=60°,
∴点A、C、P、E四点共圆,
∴∠EAC=∠EPC,
∵∠APC=∠B+∠BAP,∠APE=∠B,
∴∠BAP=∠CAE,
∴∠PAE=60°,
∴△APE是等边三角形,
∴AP=PE.
(2)连接AE,取AG=CP,连接GP.
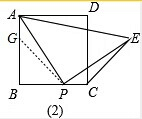
∵∠EPC+∠APB=90°,∠APB+∠PAB=90°,
∴∠EPC=∠PAB,
∵AB=BC,AG=PC,
∴BG=BP,
∴∠BGP=45°,
∴∠AGP=135°,
∵∠ECP=∠BCD+∠ECD=135°,
∴∠AGP=∠ECP,
在△AGP和△PCE中,
,
∴△AGP≌△PCE(ASA),
∴AP=PE.

∵CE是等边△ABC的外角平分线,
∴∠ACE=∠DCE=60°,
∴点A、C、P、E四点共圆,
∴∠EAC=∠EPC,
∵∠APC=∠B+∠BAP,∠APE=∠B,
∴∠BAP=∠CAE,
∴∠PAE=60°,
∴△APE是等边三角形,
∴AP=PE.
(2)连接AE,取AG=CP,连接GP.

∵∠EPC+∠APB=90°,∠APB+∠PAB=90°,
∴∠EPC=∠PAB,
∵AB=BC,AG=PC,
∴BG=BP,
∴∠BGP=45°,
∴∠AGP=135°,
∵∠ECP=∠BCD+∠ECD=135°,
∴∠AGP=∠ECP,
在△AGP和△PCE中,
|
∴△AGP≌△PCE(ASA),
∴AP=PE.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中构建全等三角形并证明是解题的关键.

练习册系列答案
相关题目
 如图,正方形ABCD的对角线相交于O,点F在AD上,AD=3AF,△AOF的外接圆交AB于E,则
如图,正方形ABCD的对角线相交于O,点F在AD上,AD=3AF,△AOF的外接圆交AB于E,则| AE |
| AF |
A、
| ||
| B、3 | ||
C、
| ||
| D、2 |
 半径为2,AB为直径,C、D是
半径为2,AB为直径,C、D是
 一条笔直的大街宽是50米,一条人行道穿过这条大街并与大街成某一角度,人行道的宽度是14米,长度是60米,求人行道间的距离.
一条笔直的大街宽是50米,一条人行道穿过这条大街并与大街成某一角度,人行道的宽度是14米,长度是60米,求人行道间的距离.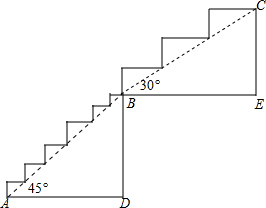 某阶梯的形状如图所示,其中线段AB=BC,AB部分的坡角为45°,BC部分的坡角为30°,AD=1.5m.如果每个台阶的高不超过20cm,那么这一阶梯至少有多少个台阶?(最后一个台阶的高不足20cm时,按一个台阶计算)
某阶梯的形状如图所示,其中线段AB=BC,AB部分的坡角为45°,BC部分的坡角为30°,AD=1.5m.如果每个台阶的高不超过20cm,那么这一阶梯至少有多少个台阶?(最后一个台阶的高不足20cm时,按一个台阶计算)