题目内容
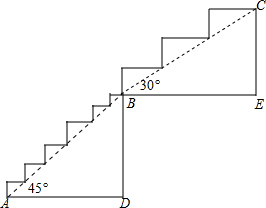 某阶梯的形状如图所示,其中线段AB=BC,AB部分的坡角为45°,BC部分的坡角为30°,AD=1.5m.如果每个台阶的高不超过20cm,那么这一阶梯至少有多少个台阶?(最后一个台阶的高不足20cm时,按一个台阶计算)
某阶梯的形状如图所示,其中线段AB=BC,AB部分的坡角为45°,BC部分的坡角为30°,AD=1.5m.如果每个台阶的高不超过20cm,那么这一阶梯至少有多少个台阶?(最后一个台阶的高不足20cm时,按一个台阶计算)考点:解直角三角形的应用-坡度坡角问题
专题:
分析:根据含30度的直角三角形三边的关系和等腰直角三角形的性质得到AB和BC的长,二者的和乘以100后除以20即可确定台阶的数.
解答:解:∵AB部分的坡角为45°,AD=1.5m,
∴BD=AD=1.5m,
∴AB=
米,
∵AB=BC,
∴BC=
米,
∵BC部分的坡角为30°,
∴EC=
BC=
m,
∴BD+CE=
+
(m),
∵每个台阶的高不超过20cm,
∴共需台阶(
+
)×100÷20≈13.
∴BD=AD=1.5m,
∴AB=
| 3 |
| 2 |
| 2 |
∵AB=BC,
∴BC=
| 3 |
| 2 |
| 2 |
∵BC部分的坡角为30°,
∴EC=
| 1 |
| 2 |
3
| ||
| 4 |
∴BD+CE=
| 3 |
| 2 |
3
| ||
| 4 |
∵每个台阶的高不超过20cm,
∴共需台阶(
| 3 |
| 2 |
| 3 |
| 4 |
| 2 |
点评:本题考查了坡度的概念:斜坡的坡度等于斜坡的铅直高度与对应的水平距离的比值,即斜坡的坡度等于斜坡的坡角的正弦.也考查了含30度的直角三角形三边的关系和等腰直角三角形的性质.

练习册系列答案
相关题目
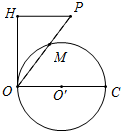 如图,点P为⊙O′外一点,OC为⊙O′的直径,PO=OC,PO交⊙O于M,OH为⊙O′的切线,且PH⊥OH.
如图,点P为⊙O′外一点,OC为⊙O′的直径,PO=OC,PO交⊙O于M,OH为⊙O′的切线,且PH⊥OH.
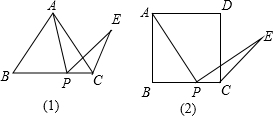 (1)在正△ABC中,P在BC上,∠APE=∠B,PE与∠C的外角平分线交于E,求证:AP=PE.
(1)在正△ABC中,P在BC上,∠APE=∠B,PE与∠C的外角平分线交于E,求证:AP=PE.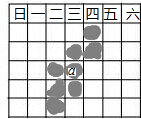 如图是一张日历表,打阴影的8个数字的和是135,中间这个数a是
如图是一张日历表,打阴影的8个数字的和是135,中间这个数a是