题目内容
抛物线y=-
(x+1)2的对称轴是 .
| 1 |
| 4 |
考点:二次函数的性质
专题:
分析:根据抛物线的顶点式方程y=-
(x+1)2可以直接写出它的对称轴直线方程.
| 1 |
| 4 |
解答:解:∵抛物线y=-
(x+1)2的对称轴直线是该图象的顶点坐标的横坐标,
∴x=-1;
故答案是:x=-1.
| 1 |
| 4 |
∴x=-1;
故答案是:x=-1.
点评:本题考查了二次函数的性质.抛物线的顶点式方程为y=a(x-h)2+k,顶点坐标是(h,k),对称轴是x=h.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
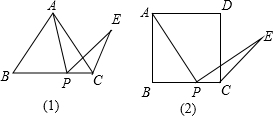 (1)在正△ABC中,P在BC上,∠APE=∠B,PE与∠C的外角平分线交于E,求证:AP=PE.
(1)在正△ABC中,P在BC上,∠APE=∠B,PE与∠C的外角平分线交于E,求证:AP=PE.(2)如图(2),(1)中“在正△ABC 中“改为“在正方形ABCD中“,其余不变,其结论仍然成立吗?
已知一次函数y=kx+b(k≠0)经过(3,-1)、(-6,5)两点,则它的图象不经过( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
在某次聚会上每两个人都握了一次手,所有人共握手28次.设有x人参加这次聚会,则列出方程正确的是( )
| A、x(x-1)=28 | ||
B、
| ||
| C、x(x+1)=28 | ||
D、
|
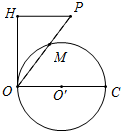 如图,点P为⊙O′外一点,OC为⊙O′的直径,PO=OC,PO交⊙O于M,OH为⊙O′的切线,且PH⊥OH.
如图,点P为⊙O′外一点,OC为⊙O′的直径,PO=OC,PO交⊙O于M,OH为⊙O′的切线,且PH⊥OH.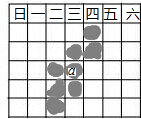 如图是一张日历表,打阴影的8个数字的和是135,中间这个数a是
如图是一张日历表,打阴影的8个数字的和是135,中间这个数a是