题目内容
11.(1)42×$(-\frac{2}{3})÷\frac{7}{2}$-(-12)÷(-4)(2)(-1)2012+(-$\frac{1}{2}$)3÷(-2)×8
(3)-22-[-($\frac{1}{2}$)3]2+(-2)3-(-1)2
(4)[30-($\frac{7}{9}$+$\frac{5}{6}-\frac{11}{12}$)×36]÷(-5)
(5)10x2+[2x-(5+4x2-x)-4]
(6)a3-5-(a2-3a)+(3a2-3+6a3)
分析 (1)先算乘除,再算加减即可;
(2)先算乘方,再算乘除,最后算加减即可;
(3)先算乘方,再算加减即可;
(4)先把小括号中的每一项分别同36相乘,再算大括号里的面的,最后再算除法即可;
(5)、(6)先去括号,再合并同类项即可.
解答 解:(1)原式=-28×$\frac{2}{7}$-3
=-8-3
=-11;
(2)原式=1-$\frac{1}{8}$×(-$\frac{1}{2}$)×8
=1+$\frac{1}{2}$
=$\frac{3}{2}$;
(3)原式=-4-$\frac{1}{64}$-8-1
=-13-$\frac{1}{64}$
=-13$\frac{1}{64}$;
(4)原式=[30-$\frac{7}{9}$×36-$\frac{5}{6}$×36+$\frac{11}{12}$×36]÷(-5)
=[30-28-30+33]÷(-5)
=5×(-$\frac{1}{5}$)
=-1;
(5)原式=10x2+2x-5-4x2+x-4
=6x2+3x-9;
(6)原式=a3-5-a2+3a+3a2-3+6a3
=7a3+2a2+3a-8.
点评 本题考查的是有理数的混合运算,熟记有理数混合运算的法则是解答此题的关键.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
19.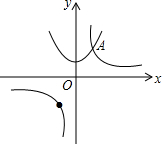 如图,抛物线y=x2+1与双曲线y=$\frac{k}{x}$的交点A的横坐标是1,则关于x的不等式$\frac{k}{x}<{x^2}$+1的解集是( )
如图,抛物线y=x2+1与双曲线y=$\frac{k}{x}$的交点A的横坐标是1,则关于x的不等式$\frac{k}{x}<{x^2}$+1的解集是( )
 如图,抛物线y=x2+1与双曲线y=$\frac{k}{x}$的交点A的横坐标是1,则关于x的不等式$\frac{k}{x}<{x^2}$+1的解集是( )
如图,抛物线y=x2+1与双曲线y=$\frac{k}{x}$的交点A的横坐标是1,则关于x的不等式$\frac{k}{x}<{x^2}$+1的解集是( )| A. | x>1 | B. | x<0 | C. | 0<x<1 | D. | x<0或x>1 |
20.规定一种新的运算:a△b=a•b-a-b+1,比如3△4=3×4-3-4+1=6.则(-3)△x的值为( )
| A. | -4x+4 | B. | -4x-2 | C. | -x+1 | D. | -2x+2 |
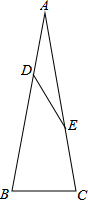 在△ABC中,AB=AC,点D在AB上,点E在AC上,且AD=DE=EC=BC.求证:∠BAC=20°.
在△ABC中,AB=AC,点D在AB上,点E在AC上,且AD=DE=EC=BC.求证:∠BAC=20°.