题目内容
17.已知一个等腰三角形的两边长分别为$\sqrt{18}$和$\sqrt{50}$,则这个等腰三角形的周长为( )| A. | 11$\sqrt{2}$ | B. | 13$\sqrt{2}$ | C. | 11$\sqrt{3}$或$\sqrt{3}$ | D. | 11$\sqrt{2}$或13$\sqrt{2}$ |
分析 题目给出等腰三角形有两条边长为$\sqrt{18}$和$\sqrt{50}$,而没有明确腰、底分别是多少,所以要进行讨论,还要应用三角形的三边关系验证能否组成三角形.
解答 解:①$\sqrt{18}$和是腰长时,能组成三角形,周长=$\sqrt{18}$+$\sqrt{18}$+$\sqrt{50}$=11$\sqrt{2}$,
②5是腰长时,能组成三角形,周长=$\sqrt{50}$+$\sqrt{50}$+$\sqrt{18}$=13$\sqrt{2}$,
故这个等腰三角形的周长为11$\sqrt{2}$或13$\sqrt{2}$.
故选:D.
点评 本题考查了等腰三角形的性质和三角形的三边关系;已知没有明确腰和底边的题目一定要想到两种情况,分类进行讨论,还应验证各种情况是否能构成三角形进行解答,这点非常重要,也是解题的关键.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案
相关题目
7.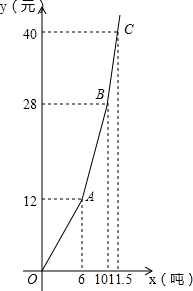 为了加强公民的节水意识,合理利用水资源,某区采用价格调控手段以期待达到节水的目的,图是此区自来水厂对居民某月用水量x吨与水费y元的函数图象(水费按月结算).
为了加强公民的节水意识,合理利用水资源,某区采用价格调控手段以期待达到节水的目的,图是此区自来水厂对居民某月用水量x吨与水费y元的函数图象(水费按月结算).
(1)填空
价目表
(2)若某户居民9月份用水量为9.5吨,求该用户9月份水费;
(3)若某户居民10月份水费30元,求该用户10月份用水量;
(4)若某户居民11月、12月共用水18吨,其中11月用水a(吨),用含a的代数式表示该户居民11月、12月共应交水费Q(元).
 为了加强公民的节水意识,合理利用水资源,某区采用价格调控手段以期待达到节水的目的,图是此区自来水厂对居民某月用水量x吨与水费y元的函数图象(水费按月结算).
为了加强公民的节水意识,合理利用水资源,某区采用价格调控手段以期待达到节水的目的,图是此区自来水厂对居民某月用水量x吨与水费y元的函数图象(水费按月结算).(1)填空
价目表
| 每月水用量 | 单价 |
| 不超出6吨的部分 | 2元/吨 |
| 超出6吨不超出10吨的部分 | 4 元/吨 |
| 超出10吨的部分 | 8元/吨 |
(3)若某户居民10月份水费30元,求该用户10月份用水量;
(4)若某户居民11月、12月共用水18吨,其中11月用水a(吨),用含a的代数式表示该户居民11月、12月共应交水费Q(元).
8.若一次函数y=(m-3)x+5的函数值,y随x的增大而增大,则( )
| A. | m<0 | B. | m>0 | C. | m<3 | D. | m>3 |
5. 如图,已知AE=CF,∠AFD=∠CEB,添加一个条件后,仍无法判定△ADF≌△CBE的是( )
如图,已知AE=CF,∠AFD=∠CEB,添加一个条件后,仍无法判定△ADF≌△CBE的是( )
 如图,已知AE=CF,∠AFD=∠CEB,添加一个条件后,仍无法判定△ADF≌△CBE的是( )
如图,已知AE=CF,∠AFD=∠CEB,添加一个条件后,仍无法判定△ADF≌△CBE的是( )| A. | ∠A=∠C | B. | AD=CB | C. | BE=DF | D. | AD∥BC |
12. 在下列软件的图标中,其中是中心对称图形的有( )
在下列软件的图标中,其中是中心对称图形的有( )
 在下列软件的图标中,其中是中心对称图形的有( )
在下列软件的图标中,其中是中心对称图形的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
9.函数y=$\frac{x}{3-x}$的自变量取值范围是( )
| A. | x≠3 | B. | x≠0 | C. | x≠3且x≠0 | D. | x<3 |
6.下列关于图形旋转的说法不正确的是( )
| A. | 对应点到旋转中心的距离相等 | |
| B. | 对应点与旋转中心所连线段的夹角等于旋转角 | |
| C. | 旋转前后的图形全等 | |
| D. | 旋转后,图形的大小,形状与位置都发生了变化 |
7. 如图,直线l1:y=x-4与直线l2:y=-$\frac{4}{3}$x+3相交于点(3,-1),则方程组$\left\{\begin{array}{l}{\frac{x}{2}-\frac{y}{2}=2}\\{x+\frac{3y}{4}=\frac{9}{4}}\end{array}\right.$的解是( )
如图,直线l1:y=x-4与直线l2:y=-$\frac{4}{3}$x+3相交于点(3,-1),则方程组$\left\{\begin{array}{l}{\frac{x}{2}-\frac{y}{2}=2}\\{x+\frac{3y}{4}=\frac{9}{4}}\end{array}\right.$的解是( )
 如图,直线l1:y=x-4与直线l2:y=-$\frac{4}{3}$x+3相交于点(3,-1),则方程组$\left\{\begin{array}{l}{\frac{x}{2}-\frac{y}{2}=2}\\{x+\frac{3y}{4}=\frac{9}{4}}\end{array}\right.$的解是( )
如图,直线l1:y=x-4与直线l2:y=-$\frac{4}{3}$x+3相交于点(3,-1),则方程组$\left\{\begin{array}{l}{\frac{x}{2}-\frac{y}{2}=2}\\{x+\frac{3y}{4}=\frac{9}{4}}\end{array}\right.$的解是( )| A. | $\left\{\begin{array}{l}{x=3}\\{y=-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-1}\\{y=3}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=-1}\\{y=-3}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$ |