题目内容
19. 工人师傅常用角尺平分一个任意角.做法如下:如图,∠AOB是一个任意角,在边OA、OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度与M、N重合,过角尺顶点C作射线OC.那么判定△MOC≌△NOC的依据是( )
工人师傅常用角尺平分一个任意角.做法如下:如图,∠AOB是一个任意角,在边OA、OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度与M、N重合,过角尺顶点C作射线OC.那么判定△MOC≌△NOC的依据是( )| A. | 边角边 | B. | 边边边 | C. | 角边角 | D. | 角角边 |
分析 利用全等三角形判定定理AAS、SAS、ASA、SSS对△MOC和△NOC进行分析,即可作出正确选择.
解答 解:在△MOC与△NOC中,
$\left\{\begin{array}{l}{OM=ON}\\{CM=CN}\\{OC=OC}\end{array}\right.$,
∴△MOC≌△NOC(SSS).
故选B.
点评 本题考查了全等三角形的判定定理的应用,能正确应用全等三角形的判定定理进行推理是解此题的关键,难度适中.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.一天,小明在家和学校之间行走,为了好奇,他测了一下在无风时的速度是50米/分,从家到学校用了15分钟,从原路返回用了18分钟20秒.设风的速度是x米/分,则所列方程为( )
| A. | 15(50+x)=18.2(50-x) | B. | 15(50-x)=18.2(50+x) | C. | 15(50+x)=$\frac{55}{3}$(50-x) | D. | 15(50-x)=$\frac{55}{3}$(50+x) |
14.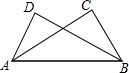 如图,已知△ABC≌△BAD,A和B,C和D分别是对应顶点,且∠C=60°,∠ABD=35°,则∠BAD的度数是( )
如图,已知△ABC≌△BAD,A和B,C和D分别是对应顶点,且∠C=60°,∠ABD=35°,则∠BAD的度数是( )
 如图,已知△ABC≌△BAD,A和B,C和D分别是对应顶点,且∠C=60°,∠ABD=35°,则∠BAD的度数是( )
如图,已知△ABC≌△BAD,A和B,C和D分别是对应顶点,且∠C=60°,∠ABD=35°,则∠BAD的度数是( )| A. | 60° | B. | 35° | C. | 85° | D. | 不能确定 |
4.如果不等式组$\left\{\begin{array}{l}{-4x+1<-8-x}\\{x>m}\end{array}\right.$的解集是x>m,那么m的取值范围是( )
| A. | m≥3 | B. | m≤3 | C. | m=3 | D. | m<3 |
9.在同一平面坐标系中,抛物线y=-x2+2x-3通过平移得到的抛物线为y=-x2-4x+1,下面对抛物线y=-x2+2x-3平移得到的抛物线y=-x2-4x+1的描述正确的是( )
| A. | 向右平移3个单位,再向上平移7个单位 | |
| B. | 向左平移3个单位,再向上平移7个单位 | |
| C. | 向右平移3个单位,再向下平移7个单位 | |
| D. | 向左平移3个单位,再向下平移7个单位 |
 如图,已知在矩形ABCD中,AB=12,BC=16,⊙O1和⊙O2分别是△ABC和△ADC的内切圆,点E、F为切点,则EF的长是4$\sqrt{5}$cm.
如图,已知在矩形ABCD中,AB=12,BC=16,⊙O1和⊙O2分别是△ABC和△ADC的内切圆,点E、F为切点,则EF的长是4$\sqrt{5}$cm.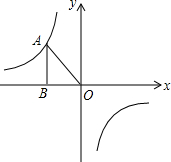 已知如图,反比例函数y=-$\frac{6}{x}$的图象上有一点A(-2,■),它的纵坐标被墨水污染了,根据题意,解答下列问题.
已知如图,反比例函数y=-$\frac{6}{x}$的图象上有一点A(-2,■),它的纵坐标被墨水污染了,根据题意,解答下列问题.