题目内容
14.先化简,再求值:$\frac{{{a^2}-{b^2}}}{a}÷(a-\frac{{2ab-{b^2}}}{a})$,其中,a=1+$\sqrt{2}$,b=1-$\sqrt{2}$.分析 先把括号内通分,再把分子分母因式分解和除法运算化为乘法运算,然后约分得到原式=$\frac{a+b}{a-b}$,再把a和b的值代入计算.
解答 解:原式=$\frac{(a+b)(a-b)}{a}$÷$\frac{{a}^{2}-2ab+{b}^{2}}{a}$
=$\frac{(a+b)(a-b)}{a}$•$\frac{a}{(a-b)^{2}}$
=$\frac{a+b}{a-b}$,
当a=1+$\sqrt{2}$,b=1-$\sqrt{2}$,原式=$\frac{1+\sqrt{2}+1-\sqrt{2}}{1+\sqrt{2}-1+\sqrt{2}}$=$\frac{2}{2\sqrt{2}}$=$\frac{\sqrt{2}}{2}$.
点评 本题考查了分式的化简求值:先把分式化简后,再把分式中未知数对应的值代入求出分式的值.在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
19.实数-2的绝对值是( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | $-\frac{1}{2}$ | D. | -2 |
3.我国古代问题:以绳测井,若将绳三折测之,绳多四尺;若将绳四折测之,绳多一尺,绳长、井深各几何?(注:绳儿折即把绳平均分成几等分.)( )
| A. | 36,8 | B. | 28,6 | C. | 28,8 | D. | 13,3 |
12.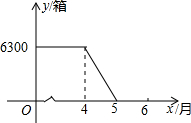 某工厂生产空气清新剂,今年4月份后,每天的产量与销售量均为500箱,进入4月份后,每天的产量保持不变,市场需求量不断增加.如图是四月前后一段时期库存量y(箱)与生产时间t(月份)之间的函数图象.
某工厂生产空气清新剂,今年4月份后,每天的产量与销售量均为500箱,进入4月份后,每天的产量保持不变,市场需求量不断增加.如图是四月前后一段时期库存量y(箱)与生产时间t(月份)之间的函数图象.
(1)从图象可知,该厂5月份开始出现零库存:此时日产销量为500箱;
(2)4月份总共的销售量为21300箱;
(3)为满足市场需求,该厂打算在投资不超过135万元的情况下,购买5台新设备,使扩大生产规模后的日产量不低于4月份的平均日销售量.现有A、B两种型号的设备可供选择,其价格与两种设备的日产量如下表:
求:有几种购买设备的方案?若为了使日产量最大,应选择怎样的方案?
 某工厂生产空气清新剂,今年4月份后,每天的产量与销售量均为500箱,进入4月份后,每天的产量保持不变,市场需求量不断增加.如图是四月前后一段时期库存量y(箱)与生产时间t(月份)之间的函数图象.
某工厂生产空气清新剂,今年4月份后,每天的产量与销售量均为500箱,进入4月份后,每天的产量保持不变,市场需求量不断增加.如图是四月前后一段时期库存量y(箱)与生产时间t(月份)之间的函数图象.(1)从图象可知,该厂5月份开始出现零库存:此时日产销量为500箱;
(2)4月份总共的销售量为21300箱;
(3)为满足市场需求,该厂打算在投资不超过135万元的情况下,购买5台新设备,使扩大生产规模后的日产量不低于4月份的平均日销售量.现有A、B两种型号的设备可供选择,其价格与两种设备的日产量如下表:
| 型号 | A | B |
| 价格(万元/台) | 28 | 25 |
| 日产量(箱/台) | 50 | 40 |
 在综合实践课上,小明同学设计了如图测河塘宽AB的方案:在河塘外选一点O,连结AO,BO,测得AO=18m,BO=21m,延长AO,BO分别到D,C两点,使OC=6m,OD=7m,又测得CD=5m,则河塘宽AB=15m.
在综合实践课上,小明同学设计了如图测河塘宽AB的方案:在河塘外选一点O,连结AO,BO,测得AO=18m,BO=21m,延长AO,BO分别到D,C两点,使OC=6m,OD=7m,又测得CD=5m,则河塘宽AB=15m.