题目内容
19.如图1,这个图案是我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.此图案的示意图如图2,其中四边形ABCD和四边形EFGH都是正方形,△ABF、△BCG、△CDH、△DAE是四个全等的直角三角形.若EF=2,DE=8,则AB的长为10.
分析 在直角△ABF中,利用勾股定理进行解答即可.
解答 解:依题意知,BG=AF=DE=8,EF=FG=2
∴BF=BG-BF=6,
∴直角△ABF中,利用勾股定理得:AB=$\sqrt{A{F}^{2}+B{F}^{2}}$=$\sqrt{{8}^{2}+{6}^{2}}$=10.
故答案是:10.
点评 此题考查勾股定理的证明,解题的关键是得到直角△ABF的两直角边的长度.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目
14. 如图,在△ABC中,点D在AB上,点E在AC上,DE∥BC.若∠A=62°,∠AED=54°,则∠B的大小为( )
如图,在△ABC中,点D在AB上,点E在AC上,DE∥BC.若∠A=62°,∠AED=54°,则∠B的大小为( )
 如图,在△ABC中,点D在AB上,点E在AC上,DE∥BC.若∠A=62°,∠AED=54°,则∠B的大小为( )
如图,在△ABC中,点D在AB上,点E在AC上,DE∥BC.若∠A=62°,∠AED=54°,则∠B的大小为( )| A. | 54° | B. | 62° | C. | 64° | D. | 74° |
4. 如图,直线a∥b,Rt△ABC的直角顶点B落在直线a上,若∠1=25°,则∠2的大小为( )
如图,直线a∥b,Rt△ABC的直角顶点B落在直线a上,若∠1=25°,则∠2的大小为( )
 如图,直线a∥b,Rt△ABC的直角顶点B落在直线a上,若∠1=25°,则∠2的大小为( )
如图,直线a∥b,Rt△ABC的直角顶点B落在直线a上,若∠1=25°,则∠2的大小为( )| A. | 55° | B. | 75° | C. | 65° | D. | 85° |
11. 如图,OM=2,MN=6,A为射线ON上的动点,以OA为一边作内角∠OAB=120°的菱形OABC,则BM+BN的最小值为( )
如图,OM=2,MN=6,A为射线ON上的动点,以OA为一边作内角∠OAB=120°的菱形OABC,则BM+BN的最小值为( )
 如图,OM=2,MN=6,A为射线ON上的动点,以OA为一边作内角∠OAB=120°的菱形OABC,则BM+BN的最小值为( )
如图,OM=2,MN=6,A为射线ON上的动点,以OA为一边作内角∠OAB=120°的菱形OABC,则BM+BN的最小值为( )| A. | $\sqrt{26}$ | B. | 6 | C. | 2$\sqrt{13}$ | D. | 2$\sqrt{15}$ |
8.如图所示的正三棱柱,它的主视图、俯视图、左视图的顺序是( )


| A. | ①②③ | B. | ②①③ | C. | ③①② | D. | ①③② |
 如图,在四边形ABCD中,AB∥CD,点E、F是对角线AC上两点,且∠ABF=∠CDE,AE=CF
如图,在四边形ABCD中,AB∥CD,点E、F是对角线AC上两点,且∠ABF=∠CDE,AE=CF 如图,点A在双曲线y=$\frac{\sqrt{3}}{x}$(x>0)上,过点A作AC⊥x轴,垂足为C,OA的垂直平分线交OC于点B,当AC=1时,△ABC的周长为$\sqrt{3}$+1.
如图,点A在双曲线y=$\frac{\sqrt{3}}{x}$(x>0)上,过点A作AC⊥x轴,垂足为C,OA的垂直平分线交OC于点B,当AC=1时,△ABC的周长为$\sqrt{3}$+1.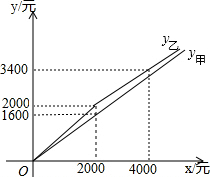 江汉平原享有“中国小龙虾之乡”的美称,甲、乙两家农贸商店,平时以同样的价格出售品质相同的小龙虾.“龙虾节”期间,甲、乙两家商店都让利酬宾,付款金额y甲、y乙(单位:元)与原价x(单位:元)之间的函数关系如图所示.
江汉平原享有“中国小龙虾之乡”的美称,甲、乙两家农贸商店,平时以同样的价格出售品质相同的小龙虾.“龙虾节”期间,甲、乙两家商店都让利酬宾,付款金额y甲、y乙(单位:元)与原价x(单位:元)之间的函数关系如图所示.