题目内容
14. 如图,在△ABC中,点D在AB上,点E在AC上,DE∥BC.若∠A=62°,∠AED=54°,则∠B的大小为( )
如图,在△ABC中,点D在AB上,点E在AC上,DE∥BC.若∠A=62°,∠AED=54°,则∠B的大小为( )| A. | 54° | B. | 62° | C. | 64° | D. | 74° |
分析 根据平行线的性质得到∠C=∠AED=54°,根据三角形的内角和即可得到结论.
解答 解:∵DE∥BC,
∴∠C=∠AED=54°,
∵∠A=62°,
∴∠B=180°-∠A-∠C=64°,
故选C.
点评 本题考查了平行线的性质,三角形的内角和,熟练掌握三角形的内角和是解题的关键.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
6.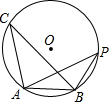 如图,△ABC是⊙O的内接三角形,∠C=30°,⊙O的半径为5,若点P是⊙O上的一点,在△ABP中,PB=AB,则PA的长为( )
如图,△ABC是⊙O的内接三角形,∠C=30°,⊙O的半径为5,若点P是⊙O上的一点,在△ABP中,PB=AB,则PA的长为( )
 如图,△ABC是⊙O的内接三角形,∠C=30°,⊙O的半径为5,若点P是⊙O上的一点,在△ABP中,PB=AB,则PA的长为( )
如图,△ABC是⊙O的内接三角形,∠C=30°,⊙O的半径为5,若点P是⊙O上的一点,在△ABP中,PB=AB,则PA的长为( )| A. | 5 | B. | $\frac{5\sqrt{3}}{2}$ | C. | 5$\sqrt{2}$ | D. | 5$\sqrt{3}$ |
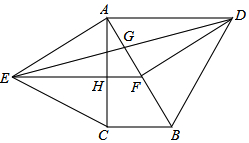 如图,分别以Rt△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB边的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.
如图,分别以Rt△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB边的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.
 如图,小明家在学校O的北偏东60°方向,距离学校80米的A处,小华家在学校O的南偏东45°方向的B处,小华家在小明家正南方向,求小华家到学校的距离.(结果精确到1米,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,$\sqrt{6}$≈2.45)
如图,小明家在学校O的北偏东60°方向,距离学校80米的A处,小华家在学校O的南偏东45°方向的B处,小华家在小明家正南方向,求小华家到学校的距离.(结果精确到1米,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,$\sqrt{6}$≈2.45)