题目内容
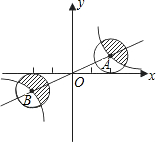 如图,正比例函数与反比例函数的图象相交于AB、两点,分别以AB、两点为圆心,画与x轴相切的两个圆,若点A的坐标为(2,1),则图中两个阴影部分面积的和是( )
如图,正比例函数与反比例函数的图象相交于AB、两点,分别以AB、两点为圆心,画与x轴相切的两个圆,若点A的坐标为(2,1),则图中两个阴影部分面积的和是( )A、
| ||
B、
| ||
| C、π | ||
| D、4π |
考点:反比例函数图象的对称性
专题:计算题
分析:先利用切线的性质得到⊙A的半径为1,再根据反比例回事图象的对称性得到点B的坐标为(-2,-1),同理得到⊙B的半径为1,则可判断⊙A与⊙B关于原点中心对称,⊙A的阴影部分与⊙B空白的部分的面积相等,所以图中两个阴影部分面积的和等于⊙A的面积,然后根据圆的面积公式计算.
解答:解:∵点A的坐标为(2,1),且⊙A与x轴相切,
∴⊙A的半径为1,
∵点A和点B是正比例函数与反比例函数的图象的交点,
∴点B的坐标为(-2,-1),
同理得到⊙B的半径为1,
∴⊙A与⊙B关于原点中心对称,
∴⊙A的阴影部分与⊙B空白的部分完全重合,
∴⊙A的阴影部分与⊙B空白的部分的面积相等,
∴图中两个阴影部分面积的和=π•12=π.
故选C.
∴⊙A的半径为1,
∵点A和点B是正比例函数与反比例函数的图象的交点,
∴点B的坐标为(-2,-1),
同理得到⊙B的半径为1,
∴⊙A与⊙B关于原点中心对称,
∴⊙A的阴影部分与⊙B空白的部分完全重合,
∴⊙A的阴影部分与⊙B空白的部分的面积相等,
∴图中两个阴影部分面积的和=π•12=π.
故选C.
点评:本题考查了反比例函数图象的对称性:反比例函数图象既是轴对称图形又是中心对称图形,对称轴分别是:①第二、四象限的角平分线y=-x;②第一、三象限的角平分线y=x;对称中心是:坐标原点.

练习册系列答案
相关题目
下列说法中正确的是( )
| A、若a⊥b,b⊥c,则a⊥c |
| B、在同一平面内,不相交的两条线段必平行 |
| C、两条直线被第三条直线所截,所得的同位角相等 |
| D、两条平行线被第三条直线所截,一对内错角的角平分线互相平行 |
根据等式的性质,下列变形正确的是( )
A、若x=y,则
| ||||
| B、若x=y,则x-2=2-y | ||||
| C、如果2x=y,那么-6x=-3y | ||||
D、如果
|
点P(3,m)到x轴的距离是4,则m的值为( )
| A、4 | B、±4 | C、-4 | D、无法确定 |
 如图,CD为⊙O的直径,弦AB⊥CD于点E,AB=10CE,CD=52,求CE的长.
如图,CD为⊙O的直径,弦AB⊥CD于点E,AB=10CE,CD=52,求CE的长.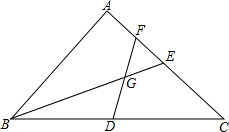 已知△ABC中,∠A=90°,AB=AC,D为BC中点,F,E为AC上两点,连接BE,DF交于△ABC内一点G,且∠EGF=45°.
已知△ABC中,∠A=90°,AB=AC,D为BC中点,F,E为AC上两点,连接BE,DF交于△ABC内一点G,且∠EGF=45°.