题目内容
如图，CD为⊙O的直径，弦AB⊥CD于点E，AB=10CE，CD=52，求CE的长．考点：垂径定理,勾股定理
专题：
分析：设CE=x，先根据CD=52求出⊙O的半径，再根据垂径定理得出AE=
AB，再根据勾股定理求出x的值即可．
| 1 |
| 2 |
解答：解：设CE=x，
∵CD为⊙O的直径，CD=52，
∴OC=26，OE=26-x．
∵弦AB⊥CD于点E，AB=10CE，
∴AE=
AB=5CE=5x．
在Rt△AOE中，
∵AE2+OE2=OA2，即（5x）2+（26-x）2=262，
解得x=2或0（舍去），即CE=2．
∵CD为⊙O的直径，CD=52，
∴OC=26，OE=26-x．
∵弦AB⊥CD于点E，AB=10CE，
∴AE=
| 1 |
| 2 |
在Rt△AOE中，
∵AE2+OE2=OA2，即（5x）2+（26-x）2=262，
解得x=2或0（舍去），即CE=2．
点评：本题考查的是垂径定理，熟知平分弦的直径平分这条弦，并且平分弦所对的两条弧是解答此题的关键．
练习册系列答案
相关题目
一个数的4
倍是-13，那么这个数为（ ）
| 1 |
| 3 |
| A、3 | ||
| B、-3 | ||
C、
| ||
D、-
|
下列语句正确的说法是（ ）
| A、两条直线相交，组成的图形是角 |
| B、从同一点引出的两条射线组成的图形也是角 |
| C、两条有公共端点的线段组成的图形叫角 |
| D、两条射线组成的图形叫角 |
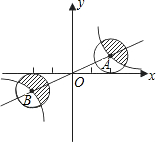如图，正比例函数与反比例函数的图象相交于AB、两点，分别以AB、两点为圆心，画与x轴相切的两个圆，若点A的坐标为（2，1），则图中两个阴影部分面积的和是（ ）