题目内容
若
+b2-b+
=0,则b-a= .
| a-3 |
| 1 |
| 4 |
考点:配方法的应用,非负数的性质:偶次方,非负数的性质:算术平方根
专题:
分析:首先利用配方法把b2-b+
=(b-
)2,进一步利用非负数的性质求得a、b,进一步代入求得答案即可.
| 1 |
| 4 |
| 1 |
| 2 |
解答:解:∵
+b2-b+
=0,
∴
+(b-
)2
=0,
∴a-3=0,b-
=0,
∴a=3,b=
,
则b-a=-
.
故答案为:-
.
| a-3 |
| 1 |
| 4 |
∴
| a-3 |
| 1 |
| 2 |
| 1 |
| 4 |
∴a-3=0,b-
| 1 |
| 2 |
∴a=3,b=
| 1 |
| 2 |
则b-a=-
| 5 |
| 2 |
故答案为:-
| 5 |
| 2 |
点评:此题考查配方法的运用,非负数的性质,掌握完全平方公式是解决问题的根本.

练习册系列答案
 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
如果a<0,b>0,a+b>0,那么下列各式中大小关系正确的是( )
| A、a<-b<-a<b |
| B、a<-b<b<-a |
| C、-b<a<b<-a |
| D、-b<a<-a<b |
下列各式中运算错误的是( )
| A、2a+a=3a |
| B、-(a-b)=-a+b |
| C、a+a2=a3 |
| D、3x2y-2yx2=x2y |
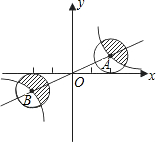 如图,正比例函数与反比例函数的图象相交于AB、两点,分别以AB、两点为圆心,画与x轴相切的两个圆,若点A的坐标为(2,1),则图中两个阴影部分面积的和是( )
如图,正比例函数与反比例函数的图象相交于AB、两点,分别以AB、两点为圆心,画与x轴相切的两个圆,若点A的坐标为(2,1),则图中两个阴影部分面积的和是( )
 如图是反比例函数的图象,O为原点,点A是图象上任意一点,AM⊥x轴,垂足为M,如果△AOM的面积为2,那么反比例函数的解析式是
如图是反比例函数的图象,O为原点,点A是图象上任意一点,AM⊥x轴,垂足为M,如果△AOM的面积为2,那么反比例函数的解析式是