题目内容
16.某通讯公司推出了A、B两种不同上网计费方式如下表:项目
| 项目/计费方式 | 月租费(元) | 限流量(MB) | 超流量(元/MB) |
| A | 5 | 30 | 0.5 |
| B | 10 | 70 | 1 |
(1)用含t的式子填写下表:
| 流量/计费方式 | t≥30 | 30≤t≤70 | t>70 |
| A种计费(元) | 5 | 0.5t-10 | 0.5t-10 |
| B种计费(元) | 10 | 10 | t-60 |
(3)当50<t<100时,你认为选择哪种计费方式更省钱,并说明理由.
分析 (1)根据两种方式的收费标准分别进行计算即可;
(2)根据两种方式的收费标准相等,列出方程计算即可;
(3)先判断出两种计费方式相等时t的值是多少,然后根据t的取值范围选择省钱的计费方式即可
解答 解:(1)填表如下:
| 流量/计费方式 | t≥30 | 30≤t≤70 | t>70 |
| A种计费(元) | 5 | 0.5t-10 | 0.5t-10 |
| B种计费(元) | 10 | 10 | t-60 |
(2)当30<t≤70时,可得:0.5t-10=10,
解得:t=40,
当t>70时,可得0.5t-10=t-60,
解得:t=100,
∴当t=40MB或t=100MB时,两种计费方式费用相等;
(3)当50<t<70时,
A种计费方式费用范围:15元<0.5t-10<25元,
B种计费方式费用还是10元,
∴B计费省钱,
当70<t<100时,
由0.5t-10>t-60,
得t<100,
∴B种计费方式更省钱,
综上所述,当50<t<100时,B种计费更省钱.
点评 此题主要考查了最优化问题的应用,解答此题的关键是求出不同的主叫时间下,两种计费方式下的花费分别是多少.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.下列计算正确的是( )
| A. | $\sqrt{25}$=±5 | B. | $\root{3}{-8}=2$ | C. | 3$\sqrt{2}$-$\sqrt{2}$=3 | D. | $\sqrt{14}$×$\sqrt{7}$=7$\sqrt{2}$ |
7.化简:
(1)(a-2b)2-(2a+b)(b-2a)-4a(a-b).
(2)($\frac{x}{{x}^{2}+2x}$-1)÷$\frac{{x}^{2}+2x+1}{{x}^{2}-4}$.
(1)(a-2b)2-(2a+b)(b-2a)-4a(a-b).
(2)($\frac{x}{{x}^{2}+2x}$-1)÷$\frac{{x}^{2}+2x+1}{{x}^{2}-4}$.
4.下列各数是无理数的是( )
| A. | 0 | B. | $\frac{1}{3}$ | C. | $\sqrt{2}$ | D. | -3 |
8.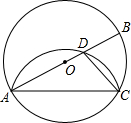 在⊙O中,AB为直径,点C为圆上一点,将劣弧$\widehat{AC}$沿弦AC翻折交AB于点D,连结CD.如图,若点D与圆心O不重合,∠BAC=25°,则∠DCA的度数( )
在⊙O中,AB为直径,点C为圆上一点,将劣弧$\widehat{AC}$沿弦AC翻折交AB于点D,连结CD.如图,若点D与圆心O不重合,∠BAC=25°,则∠DCA的度数( )
 在⊙O中,AB为直径,点C为圆上一点,将劣弧$\widehat{AC}$沿弦AC翻折交AB于点D,连结CD.如图,若点D与圆心O不重合,∠BAC=25°,则∠DCA的度数( )
在⊙O中,AB为直径,点C为圆上一点,将劣弧$\widehat{AC}$沿弦AC翻折交AB于点D,连结CD.如图,若点D与圆心O不重合,∠BAC=25°,则∠DCA的度数( )| A. | 35° | B. | 40° | C. | 45° | D. | 65° |
6.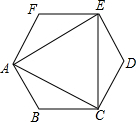 顺次连接正六边形的三个不相邻的顶点,得到如图的图形,下列说法错误的是( )
顺次连接正六边形的三个不相邻的顶点,得到如图的图形,下列说法错误的是( )
 顺次连接正六边形的三个不相邻的顶点,得到如图的图形,下列说法错误的是( )
顺次连接正六边形的三个不相邻的顶点,得到如图的图形,下列说法错误的是( )| A. | △ACE是等边三角形 | B. | 既是轴对称图形也是中心对称图形 | ||
| C. | 连接AD,则AD分别平分∠EAC与∠EDC | D. | 图中一共能画出3条对称轴 |
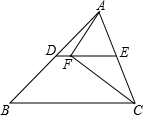 如图,在△ABC中,∠ACB=60°,点D,E分别是AB,AC的中点,点F在线段DE上,连结AF,CF.若CF恰好平分∠ACB,则∠FAC的度数为60°.
如图,在△ABC中,∠ACB=60°,点D,E分别是AB,AC的中点,点F在线段DE上,连结AF,CF.若CF恰好平分∠ACB,则∠FAC的度数为60°.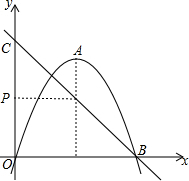 如图,抛物线y=-(x+m)2+k的顶点A的坐标为(2,4),与x轴的正半轴交于点B,点C的坐标为(0,4),点A,P关于直线BC对称.
如图,抛物线y=-(x+m)2+k的顶点A的坐标为(2,4),与x轴的正半轴交于点B,点C的坐标为(0,4),点A,P关于直线BC对称.