题目内容
16.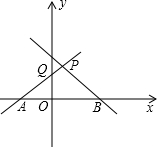 如图,直线y=x+n(n>0)交x轴于A,交y轴于Q,直线y=-2x+m(m>n)交x轴于B,交AQ于P.
如图,直线y=x+n(n>0)交x轴于A,交y轴于Q,直线y=-2x+m(m>n)交x轴于B,交AQ于P.(1)用m,n表示A,B,P的坐标;
(2)若AB=2,四边形PQOB的面积为$\frac{2}{3}$.求P点的坐标.
分析 (1)令y=0,求得两条直线与x轴的交点坐标A、B,两个函数联立方程求得交点坐标P;
(2)利用三角形PAB的面积减去三角形AOQ的面积得出四边形PQOB的面积,AB=2两个条件建立方程组求得P点坐标.
解答 解:(1)令y=0,0=x+n,x=-n,则A点坐标为(-n,0),
0=-2x+m,x=$\frac{m}{2}$,则B点坐标为($\frac{m}{2}$,0),
$\left\{\begin{array}{l}{y=x+n}\\{y=-2x+m}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=\frac{m-n}{3}}\\{y=\frac{m+2n}{3}}\end{array}\right.$,则P的坐标为($\frac{m-n}{3}$,$\frac{m+2n}{3}$);
(2)直线y=x+n与y轴的交点坐标为(0,n),
四边形PQOB的面积=$\frac{1}{2}$×2×$\frac{m+2n}{3}$-$\frac{1}{2}$×n2=$\frac{2}{3}$;
AB=m-(-n)=m+n=2,
由题意得$\left\{\begin{array}{l}{2m+4n-3{n}^{2}=4}\\{m+n=2}\end{array}\right.$
解得$\left\{\begin{array}{l}{m=2}\\{n=0}\end{array}\right.$或$\left\{\begin{array}{l}{m=\frac{4}{3}}\\{n=\frac{2}{3}}\end{array}\right.$,
∵n>0,
∴m=$\frac{4}{3}$,n=$\frac{2}{3}$.
∴P的坐标为($\frac{2}{9}$,$\frac{8}{9}$).
点评 本题考查了两直线相交或平行问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解;若两条直线是平行的关系,那么他们的自变量系数相同,即k值相同.

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 已知:如图,在Rt△ABC中,∠ACB=90°,CD是中线,CE是高,且AC2=3BC2.求证:CD、CE三等分∠ACB.
已知:如图,在Rt△ABC中,∠ACB=90°,CD是中线,CE是高,且AC2=3BC2.求证:CD、CE三等分∠ACB.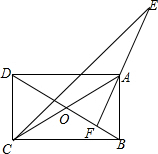 如图,已知矩形ABCD中,AC,BD交于点O,AF⊥BD垂足为F,∠BCD的平分线交FA的延长线于点E,求证:AC=AE.
如图,已知矩形ABCD中,AC,BD交于点O,AF⊥BD垂足为F,∠BCD的平分线交FA的延长线于点E,求证:AC=AE. 在所给数轴上画出表示数-3,-1,|-2|,-(-4),|0|,-|-5|的点,把这组数从小到大用”<“号连接起来.
在所给数轴上画出表示数-3,-1,|-2|,-(-4),|0|,-|-5|的点,把这组数从小到大用”<“号连接起来. 如图,在△ABC中,F、G分别是AB、AC的中点,DF⊥AB交BC于点D,EG⊥AC交AC于点G,BC=10,求△ADE周长.
如图,在△ABC中,F、G分别是AB、AC的中点,DF⊥AB交BC于点D,EG⊥AC交AC于点G,BC=10,求△ADE周长.