题目内容
6.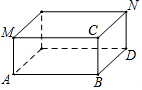 如图,有一个长方体无盖的盒子,长AB=8cm,宽BD=5cm,高BC=1cm,一只蚂蚁经过盒子里面从N爬到M.
如图,有一个长方体无盖的盒子,长AB=8cm,宽BD=5cm,高BC=1cm,一只蚂蚁经过盒子里面从N爬到M.(1)画出盒子的展开图,并画出可能最短爬行的路径;
(2)求出实际最短的爬行路径是多少厘米.
分析 要求不在同一平面内的两点间的最短距离,首先要把两点所在的两个平面展开到一个平面内,然后根据题意确定数据,再根据勾股定理即可求解.
解答  解:(1)如图所示;
解:(1)如图所示;
(2)MN=M′N′=$\sqrt{{9}^{2}+{6}^{2}}$=3$\sqrt{13}$,
MN′=$\sqrt{{8}^{2}+{7}^{2}}$=$\sqrt{113}$,
M′N=$\sqrt{1{0}^{2}+{5}^{2}}$=5$\sqrt{5}$
答:实际最短的路径$\sqrt{113}$厘米.
点评 本题的是平面展开-最短路径问题,解答此类问题时要先根据题意把立体图形展开成平面图形后,再确定两点之间的最短路径.一般情况是两点之间,线段最短.在平面图形上构造直角三角形解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.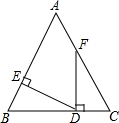 如图,在△ABC中,AB=AC,且D在BC上,DE⊥AB于E,DF⊥BC交AC于点F,若∠EDF=70°,则∠AFD的度数是( )
如图,在△ABC中,AB=AC,且D在BC上,DE⊥AB于E,DF⊥BC交AC于点F,若∠EDF=70°,则∠AFD的度数是( )
 如图,在△ABC中,AB=AC,且D在BC上,DE⊥AB于E,DF⊥BC交AC于点F,若∠EDF=70°,则∠AFD的度数是( )
如图,在△ABC中,AB=AC,且D在BC上,DE⊥AB于E,DF⊥BC交AC于点F,若∠EDF=70°,则∠AFD的度数是( )| A. | 160° | B. | 150° | C. | 140° | D. | 120° |
1.二次根式$\sqrt{2-a}$有意义,a的范围是( )
| A. | a>-2 | B. | a<-2 | C. | a=±2 | D. | a≤2 |
 如图,△ODC是由△OAB绕点O顺时针旋转30°后得到的图形,若点D恰好落在AB上,则∠BDC的度数是30°.
如图,△ODC是由△OAB绕点O顺时针旋转30°后得到的图形,若点D恰好落在AB上,则∠BDC的度数是30°.
 小明给右图建立平面直角坐标系,使医院的坐标为(0,0),火车站的坐标为(2,2).写出体育场、文化宫、超市的坐标.
小明给右图建立平面直角坐标系,使医院的坐标为(0,0),火车站的坐标为(2,2).写出体育场、文化宫、超市的坐标.