题目内容
可以由抛物线y=x2平移得到抛物线y=(x-2)2+1,下列平移方法中正确的是( )
| A、向右平移2个单位,再向上平移1个单位 |
| B、向右平移2个单位,再向下平移1个单位 |
| C、向左平移2个单位,再向上平移1个单位 |
| D、向左平移2个单位,再向下平移1个单位 |
考点:二次函数图象与几何变换
专题:计算题
分析:先根据顶点式得到抛物线y=x2的顶点坐标为(0,0),抛物线y=(x-2)2+1的顶点坐标为(2,1),然后利用顶点的平移情况得到抛物线的平移情况.
解答:解:抛物线y=x2的顶点坐标为(0,0),抛物线y=(x-2)2+1的顶点坐标为(2,1),
而点(0,0)向右平移2个单位,再向上平移1个单位得到点(2,1),
所以把抛物线y=x2向右平移2个单位,再向上平移1个单位得到抛物线y=(x-2)2+1.
故选A.
而点(0,0)向右平移2个单位,再向上平移1个单位得到点(2,1),
所以把抛物线y=x2向右平移2个单位,再向上平移1个单位得到抛物线y=(x-2)2+1.
故选A.
点评:本题考查了二次函数图象与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
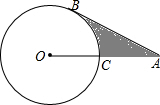 如图,AB是圆O的切线,切点为B,AO交圆O与点C,且AC=OC.
如图,AB是圆O的切线,切点为B,AO交圆O与点C,且AC=OC.
 如图,△ABC的面积为
如图,△ABC的面积为 如图,AD平分∠CAE,∠B=35°,∠DAE=60°,求∠ACD的度数.
如图,AD平分∠CAE,∠B=35°,∠DAE=60°,求∠ACD的度数. 如图,∠ADB=
如图,∠ADB= 如图,在△ABC中,AB=AC,∠BAC=120°,D为BC中点,DE⊥AB于E,AD=4,求线段BE的长度.
如图,在△ABC中,AB=AC,∠BAC=120°,D为BC中点,DE⊥AB于E,AD=4,求线段BE的长度. 有理数在数轴上的位置如图所示,用“>”,“<”符号连接:c
有理数在数轴上的位置如图所示,用“>”,“<”符号连接:c