题目内容
11.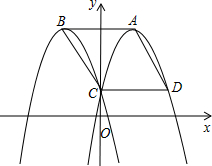 已知如图,抛物线C1:y=-x2+4x+1的顶点A在第一象限,与y轴交于点C;抛物线C2与抛物线C1关于y轴对称,其顶点为B,若点P是抛物线C1上的点,使得以A、B、C、P为顶点的四边形为平行四边形,则平行四边形ABCP的面积为8.
已知如图,抛物线C1:y=-x2+4x+1的顶点A在第一象限,与y轴交于点C;抛物线C2与抛物线C1关于y轴对称,其顶点为B,若点P是抛物线C1上的点,使得以A、B、C、P为顶点的四边形为平行四边形,则平行四边形ABCP的面积为8.
分析 先把一般式配成顶点式得到抛物线C1的顶点A的坐标为(2,5),对称轴为直线x=2,再求出C点坐标,接着利用关于y轴对称的点的坐标特征写出B点坐标,然后根据平行四边形的面积公式计算.
解答 解: 如图,
如图,
∵y=-x2+4x+1=-(x-2)2+5,
∴抛物线C1的顶点A的坐标为(2,5),对称轴为直线x=2,
∵x=0时,y=-x2+4x+1=1,
∴C点坐标为(0,1),
∵抛物线C2与抛物线C1关于y轴对称,
∴B(-2,5),
∵四边形ABCP为平行四边形,
∴平行四边形ABCP的面积=$\frac{1}{2}$•(5-1)•(2+2)=8.
故答案为8.
点评 本题考查了二次函数的性质:二次函数y=ax2+bx+c(a≠0)的顶点坐标是(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$),对称轴直线x=-$\frac{b}{2a}$.确定A点、C点和B点坐标是解决此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
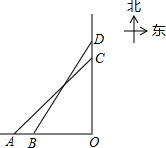 如图,轮船甲位于码头O的正西方向A处,轮船乙位于码头O的正北方向C处,此时测得轮船乙在甲的东北方向,轮船甲自西向东匀速行驶,同时轮船乙沿正北方向匀速行驶,它们的速度分别为45km/h和36km/h,经过0.1h,轮船甲行驶至B处,轮船乙行驶至D处,此时测得轮船乙在甲的北偏东32°,此时B处距离码头O多远?(结果保留一位小数)(参考数据:sin32°≈0.53,cos32°≈0.85,tan58°≈1.60,tan32°≈0.625)
如图,轮船甲位于码头O的正西方向A处,轮船乙位于码头O的正北方向C处,此时测得轮船乙在甲的东北方向,轮船甲自西向东匀速行驶,同时轮船乙沿正北方向匀速行驶,它们的速度分别为45km/h和36km/h,经过0.1h,轮船甲行驶至B处,轮船乙行驶至D处,此时测得轮船乙在甲的北偏东32°,此时B处距离码头O多远?(结果保留一位小数)(参考数据:sin32°≈0.53,cos32°≈0.85,tan58°≈1.60,tan32°≈0.625)
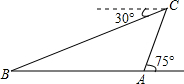 为了加快我省城乡公路建设,我省计划“十三五”期间高速公路运营里程达1000公里,进一步打造城乡快速连接通道,某地计划修建一条高速公路,需在小山东西两侧A,B之间开通一条隧道,工程技术人员乘坐热气球对小山两侧A、B之间的距离进行了测量,他们从A处乘坐热气球出发,由于受西风的影响,热气球以30米/分的速度沿与地面成75°角的方向飞行,25分钟后到达C处,此时热气球上的人测得小山西侧B点的俯角为30°,则小山东西两侧A、B两点间的距离为多少米?
为了加快我省城乡公路建设,我省计划“十三五”期间高速公路运营里程达1000公里,进一步打造城乡快速连接通道,某地计划修建一条高速公路,需在小山东西两侧A,B之间开通一条隧道,工程技术人员乘坐热气球对小山两侧A、B之间的距离进行了测量,他们从A处乘坐热气球出发,由于受西风的影响,热气球以30米/分的速度沿与地面成75°角的方向飞行,25分钟后到达C处,此时热气球上的人测得小山西侧B点的俯角为30°,则小山东西两侧A、B两点间的距离为多少米?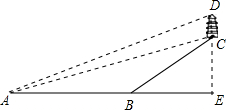 鹅岭公司是重庆最早的私家园林,前身为礼圆,是国家级AAA旅游景区,圆内有一毗胜楼,登上高楼能欣赏到重庆的优美景色,周末小嘉同学游览鹅岭公司,如图,在A点处观察到毗胜楼楼底C的仰角为12°,楼顶D的仰角为13°,测得水平距离AE=1200m,BC的坡度i=8:15
鹅岭公司是重庆最早的私家园林,前身为礼圆,是国家级AAA旅游景区,圆内有一毗胜楼,登上高楼能欣赏到重庆的优美景色,周末小嘉同学游览鹅岭公司,如图,在A点处观察到毗胜楼楼底C的仰角为12°,楼顶D的仰角为13°,测得水平距离AE=1200m,BC的坡度i=8:15
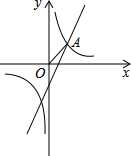 如图,己知点A是反比例函数y=$\frac{1}{x}$的图象与一次函数y=2x-1的图象在第一象限的交点,点P是x轴上一点,当△OAP为等腰三角形时,点P的坐标为($\sqrt{2}$,0),(-$\sqrt{2}$,0),(2,0),(1,0).
如图,己知点A是反比例函数y=$\frac{1}{x}$的图象与一次函数y=2x-1的图象在第一象限的交点,点P是x轴上一点,当△OAP为等腰三角形时,点P的坐标为($\sqrt{2}$,0),(-$\sqrt{2}$,0),(2,0),(1,0).