题目内容
1.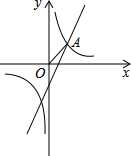 如图,己知点A是反比例函数y=$\frac{1}{x}$的图象与一次函数y=2x-1的图象在第一象限的交点,点P是x轴上一点,当△OAP为等腰三角形时,点P的坐标为($\sqrt{2}$,0),(-$\sqrt{2}$,0),(2,0),(1,0).
如图,己知点A是反比例函数y=$\frac{1}{x}$的图象与一次函数y=2x-1的图象在第一象限的交点,点P是x轴上一点,当△OAP为等腰三角形时,点P的坐标为($\sqrt{2}$,0),(-$\sqrt{2}$,0),(2,0),(1,0).
分析 把反比例函数y=$\frac{1}{x}$与一次函数y=2x-1这两个函数组成方程组求解即可得到A点坐标,然后求出OA的距离,再根据:OA=OP,OA=AP,OP=AP,分情况讨论解决.
解答 解:依题意有
$\left\{\begin{array}{l}{y=\frac{1}{x}}\\{y=2x-1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{x}_{1}=-\frac{1}{2}}\\{{y}_{1}=-2}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=1}\\{{y}_{2}=1}\end{array}\right.$,
∵点A在第一象限,
∴点A的坐标为(1,1).
∴OA=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,OA与x轴所夹锐角为45°,
①当OA为腰时,由OA=OP1得P1($\sqrt{2}$,0),
由OA=OP2得P2(-$\sqrt{2}$,0);
由OA=AP3得P3(2,0).
②当OA为底时,OP4=AP4得P4(1,0).
∴符合条件的点有4个,分别是($\sqrt{2}$,0),(-$\sqrt{2}$,0),(2,0),(1,0).
故答案为:($\sqrt{2}$,0),(-$\sqrt{2}$,0),(2,0),(1,0).
点评 本题考查了反比例函数与一次函数的交点问题,关键是理解同时在两个函数解析式上,应是这两个函数解析式的公共解.答案较多时,应有规律的去找不同的解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.下列方程中,是一元二次方程的是( )
| A. | 4x2=3y | B. | x(x+1)=5x2-1 | C. | $\sqrt{x}$-3=5x2-$\sqrt{6}$ | D. | $\frac{1}{{x}^{2}}$+3x-1=0 |
11.下列计算正确的是( )
| A. | (a+b)2=a2+b2 | B. | (3a-b)2=9a2-6ab-b2 | ||
| C. | a6b÷a2=a3b | D. | (-ab3)2=a2b6 |
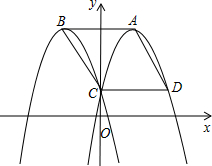 已知如图,抛物线C1:y=-x2+4x+1的顶点A在第一象限,与y轴交于点C;抛物线C2与抛物线C1关于y轴对称,其顶点为B,若点P是抛物线C1上的点,使得以A、B、C、P为顶点的四边形为平行四边形,则平行四边形ABCP的面积为8.
已知如图,抛物线C1:y=-x2+4x+1的顶点A在第一象限,与y轴交于点C;抛物线C2与抛物线C1关于y轴对称,其顶点为B,若点P是抛物线C1上的点,使得以A、B、C、P为顶点的四边形为平行四边形,则平行四边形ABCP的面积为8.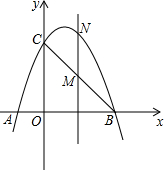 如图,已知抛物线经过点A(-1,0),B(3,0),C(0,3)三点.
如图,已知抛物线经过点A(-1,0),B(3,0),C(0,3)三点. 如图,在四边形ABCD中,∠A=90°,AD∥BC,E为AB的中点,连接CE,BD,过点E作FE⊥CE于点E,交AD于点F,连接CF,已知2AD=AB=BC.
如图,在四边形ABCD中,∠A=90°,AD∥BC,E为AB的中点,连接CE,BD,过点E作FE⊥CE于点E,交AD于点F,连接CF,已知2AD=AB=BC.