题目内容
9．下列各式中计算正确的是（ ）| A． | x2•x4=x6 | B． | 2m-（n+1）=2m-n+1 | C． | x5+2x5=3x10 | D． | （2a）3=2a3 |
分析 直接利用同底数幂的乘法运算法则以及去括号法则以及积的乘方运算法则分别化简进而求出答案．
解答 解：A、x2•x4=x6，正确；
B、2m-（n+1）=2m-n-1，故此选项错误；
C、x5+2x5=3x5，故此选项错误；
D、（2a）3=8a3，故此选项错误；
故选：A．
点评 此题主要考查了积的乘方运算、同底数幂的乘法运算以及去括号法则，正确掌握运算法则是解题关键．
练习册系列答案
相关题目
17．
如图，在平面直角坐标系中，一个正方形的中点原点O，且一组对边与y轴平行，点A（a，-4a）是反比例函数y=$\frac{k}{x}$的图象上与正方形的一个交点，若图中阴影部分的面积等于16，则k的值为（ ）
如图，在平面直角坐标系中，一个正方形的中点原点O，且一组对边与y轴平行，点A（a，-4a）是反比例函数y=$\frac{k}{x}$的图象上与正方形的一个交点，若图中阴影部分的面积等于16，则k的值为（ ）| A． | -16 | B． | -8 | C． | -4 | D． | -1 |
4．
如图是二次函数y=ax2+bx+c（a≠0）图象的一部分，对称轴为x=$\frac{1}{2}$，且经过点（2，0），有下列说法：①abc＜0；②a+b=0；③a-b+c=0；④若（0，y1），（1，y2）是抛物线上的两点，则y1=y2．上述说法正确的是（ ）
如图是二次函数y=ax2+bx+c（a≠0）图象的一部分，对称轴为x=$\frac{1}{2}$，且经过点（2，0），有下列说法：①abc＜0；②a+b=0；③a-b+c=0；④若（0，y1），（1，y2）是抛物线上的两点，则y1=y2．上述说法正确的是（ ）| A． | ①②③④ | B． | ③④ | C． | ①③④ | D． | ①② |
14．
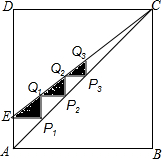如图．正方形ABCD的边长为4，点E为AD边上一点．，AE=1，连接AC，CE，过点E作AB的平行线交AC于点P1，过点P1作AD的平行线交CE于Q1，再过Q1作AB的平行线交AC于P2，…如此不断进行下去形成△AEP1，△P1Q1P2，△P2Q2P3，…，记它们的面积之和为S1，类似地形成△EP1Q1，△Q1P2Q2，△Q2P3Q3，…，记它们的面积之和为S2，则$\frac{{S}_{2}}{{S}_{1}}$的值为（ ）
如图．正方形ABCD的边长为4，点E为AD边上一点．，AE=1，连接AC，CE，过点E作AB的平行线交AC于点P1，过点P1作AD的平行线交CE于Q1，再过Q1作AB的平行线交AC于P2，…如此不断进行下去形成△AEP1，△P1Q1P2，△P2Q2P3，…，记它们的面积之和为S1，类似地形成△EP1Q1，△Q1P2Q2，△Q2P3Q3，…，记它们的面积之和为S2，则$\frac{{S}_{2}}{{S}_{1}}$的值为（ ）| A． | $\frac{3}{5}$ | B． | $\frac{3}{4}$ | C． | $\frac{4}{5}$ | D． | $\frac{5}{6}$ |
如图在Rt△ACB中，C为直角顶点，∠ABC=25°，O为斜边中点．将OA绕着点O逆时针旋转θ°（0＜θ＜180）至OP，当△BCP恰为轴对称图形时，θ的值为50°或65°或80°．
18．下列图中，不是轴对称图形的有（ ）个．
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
19．
如图，P为正方形ABCD对角线BD上一动点，若AB=2，则AP+BP+CP的最小值为（ ）
如图，P为正方形ABCD对角线BD上一动点，若AB=2，则AP+BP+CP的最小值为（ ）| A． | $\sqrt{2}$+$\sqrt{5}$ | B． | $\sqrt{2}$+$\sqrt{6}$ | C． | 4 | D． | 3$\sqrt{2}$ |